cpypyqed Tools¶

This package defines some tools to work with in Python code. These can be used to create and manipulate quantum states, or to calculate expectation values.

`tools.quantumstate`¶

This module provides an implementation for state vectors and density operators. These two classes are not direct wrappings of their C++QED counterparts to make them behave more pythonic. In fact, both these classes are derived from numpy.ndarray.

The relevant classes are:

StateVector
DensityOperator
StateVectorTrajectory

class cpypyqed.tools.quantumstate.DensityOperator¶

A class representing a quantum mechanical density operator. quantumdata::DensityOperator is automatically converted to this, but it is not a one to one wrapper.

fft(subsystems=None)¶

Return a DensityOperator where the given subsystems are Fourier transformed. This is the transformation position space -> momentum space.

Parameters:	subsystems – (optional) Sequence of ints, subsystems over which the fft is done. (Default is all)

ifft(subsystems=None)¶

Return a DensityOperator where the given subsystems are inversely Fourier transformed. This is the transformation momentum space -> position space.

Parameters:	subsystems – (optional) Sequence of ints, subsystems over which the ifft is done. (Default is all)

class cpypyqed.tools.quantumstate.QuantumState¶

This is the base class for StateVector and DensityOperator. It inherits from numpy.ndarray.

Parameters:	data (numpy.ndarray) – Anything a numpy.ndarray can beconstructed from. time (double) – (optional) A number defining the point of time when this state vector was reached. (Default is 0)

Any other argument that a numpy array takes. E.g. copy=False can be used so that the QuantumState shares the data storage with the given numpy array.

Most useful is maybe the tensor product ‘**’ which lets you easily calculate state vectors for combined systems.

class cpypyqed.tools.quantumstate.StateVector¶

A class representing a quantum mechanical state. quantumdata::StateVector is automatically converted to this, but it is not a one to one wrapper.

Usage

>>> sv = StateVector((1, 3, 7, 2), time=0.2, norm=True)
>>> sv = StateVector(numpy.arange(12).reshape(3,4))
>>> print sv
StateVector(3 x 4)
>>> print repr(sv)
StateVector([[ 0,  1,  2,  3],
       [ 4,  5,  6,  7],
       [ 8,  9, 10, 11]])

Parameters:

data – Anything that can be used to create a numpy array, e.g. a nested tuple or another numpy array.
time (double) – (optional) A number defining the point of time when this state vector was reached. (Default is 0)
norm (bool) – (optional) If set True the StateVector will be automatically normalized. (Default is False)
**kwargs – Any other argument that a numpy array takes. E.g. copy=False can be used so that the StateVector shares the data storage with the given numpy array.

Most useful is maybe the tensor product which lets you easily calculate state vectors for combined systems:

>>> sv1 = StateVector((1,2,3))
>>> sv2 = StateVector((3,4,0), norm=True)
>>> sv = sv1 ** sv2
>>> print sv
StateVector(3 x 3)
>>> print repr(sv)
StateVector([[ 0.6,  0.8,  0. ],
       [ 1.2,  1.6,  0. ],
       [ 1.8,  2.4,  0. ]])

The tensor product is abbreviated by the “**” operator.

diagexpvalue(operator, indices=None, title=None, multi=False)¶

Calculate the expectation value for the given diagonal operator.

Usage

>>> a = numpy.arange(4)
>>> print a
array([ 0.,  1.,  2.,  3.])
>>> sv = StateVector((1,2,1,4), norm=True)
>>> print sv.diagexpvalue(a)
2.45454545455

Parameters:	operator – The diagonal elements of a tensor representing an arbitrary diagonal operator in the basis of the StateVector. indices – (optional) Specifies which subsystems should be taken. If None is given the whole system is used. multi (bool) – (optional) If multi is True it is assumed that a list of operators is given. (Default is False)

Expectation values for combined systems are calculated in the following way (Assuming the operator only acts on first subsystem):

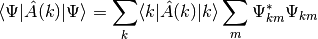
$\langle \Psi | \hat A (k) | \Psi \rangle = \sum_k \langle k | \hat A (k) | k \rangle \sum_m \Psi_{k m}^* \Psi_{k m}$

Other than the general expvalue method diagexpvalue only works for diagonal operators and only needs the diagonal elements of the matrix representation.

dyad()¶

Calculate the dyadic product with itself.

Returns:	The DensityOperator $\| \Psi \rangle \langle \Psi \|$ .

expvalue(operator, indices=None, title=None, multi=False)¶

Calculate the expectation value of the given operator.

Usage

>>> a = numpy.diag(numpy.ones(3), -1)
>>> print a
array([[ 0.,  0.,  0.,  0.],
       [ 1.,  0.,  0.,  0.],
       [ 0.,  1.,  0.,  0.],
       [ 0.,  0.,  1.,  0.]])
>>> sv = StateVector((1,2,1,2), norm=True)
>>> print sv.expvalue(a)
0.6

Parameters:	operator – A tensor representing an arbitrary operator in the basis of the StateVector. indices – (optional) Specifies which subsystems should be taken. If None is given the whole system is used. multi (bool) – (optional) If multi is True it is assumed that a list of operators is given. (Default is False)

Expectation values for combined systems are calculated in the following way (Assuming the operator only acts on first subsystem):

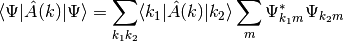
$\langle \Psi | \hat A (k) | \Psi \rangle = \sum_{k_1 k_2} \langle k_1 | \hat A (k) | k_2 \rangle \sum_m \Psi_{k_1 m}^* \Psi_{k_2 m}$

The second sum is exactly what reducesquare does while the first expression is the matrix representation of the given operator in the same basis as the StateVector.

fft(axes=None)¶

Return a StateVector where the given axes are Fourier transformed. This is the transformation position space -> momentum space.

Usage

>>> sv = StateVector((0,1,1.7,2,1.7,1,0), norm=True)
>>> print sv.fft()
StateVector(7)

Parameters:	axis – (optional) Sequence of ints, axes over which the fft is done. (Default is all)

ifft(axes=None)¶

Return a StateVector where the given axes are inversely Fourier transformed. This is the transformation momentum space -> position space.

See StateVector.fft for details.

norm()¶

Calculate the norm of the StateVector.

Usage

>>> sv = StateVector((1,2,3,4,5), norm=True)
>>> print sv.norm()
1.0

normalize()¶

Return a normalized StateVector.

Usage

>>> sv = StateVector((1,2,1,3,1))
>>> print sv.norm()
4.0
>>> nsv = sv.normalize()
>>> print nsv.norm()
1.0

outer(array)¶

Return the outer product between this and the given StateVector.

Usage

>>> sv = StateVector((0,1,2), norm=True)
>>> print repr(sv.outer(StateVector((3,4), norm=True)))
StateVector([[ 0.        ,  0.        ],
       [ 0.26832816,  0.35777088],
       [ 0.53665631,  0.71554175]])
>>> print sv.outer((3,4)) # Not normalized!
StateVector([[ 0.        ,  0.        ],
       [ 1.34164079,  1.78885438],
       [ 2.68328157,  3.57770876]])

Parameters:	array – Some kind of array (E.g. StateVector, numpy.array, list, ...).

As abbreviation sv1**sv2 can be written instead of sv1.outer(sv2).

reduce(indices, norm=True)¶

Return a StateVector where the given indices are reduced.

Usage

>>> rsv = sv.reduce(1)
>>> rsv = sv.reduce((1,2))

Parameters:	indices – An integer or a list of integers specifying over which subspaces should be summated. norm (bool) – (optional) If set True the resulting StateVector will be renormalized.

Reducing means nothing else then summing up over all given indices. E.g. a StateVector of rank 4 can be reduced to the first two indices:

>>> sv1 = StateVector((1,2), norm=True)
>>> sv2 = StateVector((1,2,3), norm=True)
>>> sv3 = StateVector((1,2,3,4,5), norm=True)
>>> sv4 = StateVector((1,2,3,4,5,6), norm=True)
>>> sv = sv1**sv2**sv3**sv4
>>> print sv
StateVector(2 x 3 x 5 x 6)
>>> print sv.reduce((2,3))
StateVector(2 x 3)

This is mathematically equivalent to:

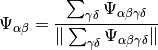
$\Psi_{\alpha \beta} = \frac {\sum_{\gamma \delta} \Psi_{\alpha \beta \gamma \delta}} {\| \sum_{\gamma \delta} \Psi_{\alpha \beta \gamma \delta} \|}$

Reducing is an easy way to find out how subspaces of a high rank state vectors behave. Don’t use reduced StateVectors for calculating expectation values - this will most likely give wrong answers!

reducesquare(indices)¶

Calculate the reduced Psi-square tensor.

Usage

>>> sv1 = StateVector((0,1,2,1,0), norm=True)
>>> sv2 = StateVector((1,0,1), norm=True)
>>> sv = sv1**sv2
>>> sqtensor = sv.reducesquare(1)

Parameters:	indices – An integer or a list of integers specifying over which subsystems should be summed up.

This method calculates the following quantity (simplified for rank 2 state vectors):

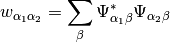
$w_{\alpha_1 \alpha_2} = \sum_\beta \Psi_{\alpha_1 \beta}^* \Psi_{\alpha_2 \beta}$

Where 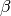$\beta$ is the reduced index.

This quantity is useful to calculate expectation values in the corresponding subspaces.

class cpypyqed.tools.quantumstate.StateVectorTrajectory¶

A class holding StateVectors for different points of time.

Parameters:

data – Some nested structure which holds state vector like arrays for different points of time.
time (double) – (optional) An array which specifies the point of time for every state vector. This array must have as many entries as there are state vectors.
**kwargs – Any other argument that a numpy array takes. E.g. copy=False can be used so that the StateVectorTrajectory shares the data storage with the given numpy array.

Most methods are simple mapped to all single StateVectors. For more documentation regarding these methods look into the docstrings of the corresponding StateVector methods.

diagexpvalue(operator, indices=None, multi=False, titles=None)¶

Calculate the expectation value of the diagonal operator for all SVs.

Returns:	An `expvalues.ExpectationValuesTrajectory` instance.

`tools.initialconditions`¶

This module provides convenient methods for creating initial conditions.

At the moment the following initial conditions are implemented:

gaussian
coherent

cpypyqed.tools.initialconditions.coherent(alpha=2, N=20)¶

Generate a coherent StateVector in the Fock space.

Usage

>>> sv = coherent(alpha=2, N=20)
>>> print sv
StateVector(20)

Parameters:	alpha – (optional) A complex number specifying the coherent state. (Default is 2) N – (optional) A number determining the dimension of the Fock space. (Default is 20)
Returns sv:	A `quantumstate.StateVector`.

The coherent state is given by the formula:

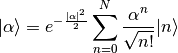
$|\alpha\rangle = e^{-\frac {|\alpha|^2} {2}} \sum_{n=0}^{N} \frac {\alpha^n} {\sqrt{n!}} |n\rangle$

Calculation is done using the recursive formula:

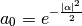
$a_0 = e^{- \frac {|\alpha|^2} {2}}$

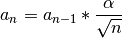
$a_n = a_{n-1} * \frac {\alpha} {\sqrt n}$

cpypyqed.tools.initialconditions.fock(dim, i)¶

Generate a Fock space basis vector.

Usage

>>> sv = fock(dim=8, i=4)
>>> print sv
StateVector(8)

Parameters:	dim (int) – Dimension of the Fock space. i (int) – Genereate the i-th basis vector
Returns sv:	A `quantumstate.StateVector`.

cpypyqed.tools.initialconditions.gaussian(x0=0, k0=0, sigma=0.5, fin=6, isItInK=False, cppqed=False)¶

Generate a StateVector with a normal distribution.

Usage

>>> sv = gaussian(x0=0.3, k0=4, sigma=0.6, fin=7)
>>> print sv
StateVector(128)

Parameters:

x0 (double) – (optional) Center in the real space.
k0 (double) – (optional) Center in the k-space.
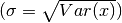sigma (double) – (optional) Width in the real space $(\sigma = \sqrt{Var(x)})$ .
fin (int) – (optional) 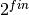$2^{fin}$ determines the amount of sample points.
isItInK (bool) – (optional) if true, sigma is interpreted as width of the wavepacket in k-space
cppqed (bool) – (optional) C++QED compatibility flag, if set to true then x0 (but not sigma) is expected in units of Pi. Defaults to False.

Returns sv:

A quantumstate.StateVector representing this gaussian wave packet in the k-space.

The generated StateVector is normalized and given in the k-space. It is the discretized and Fourier transformed of the following expression:

$\Psi(x) = \frac {1} {\sqrt[4]{2 \pi}} * \frac {1} {\sqrt{\Delta x}} e^{-\frac {x^2} {4*{\Delta x}^2}}*e^{i k_0x}$

The discretization is given by:

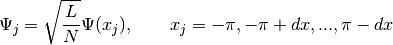
$\Psi_j = \sqrt{\frac{L}{N}} \Psi(x_j),\qquad x_j=-\pi,-\pi+dx,...,\pi-dx$

cpypyqed.tools.initialconditions.momentum_eigen(k, fin=6)¶

Generate a momentum eigenstate with momentum p in a space with finesse fin.

Usage

>>> sv = momentum_eigen(0, fin=4)
>>> print sv
StateVector(16)

Parameters:	k (int) – Wavenumber of the resulting state. fin (int) – (optional) Finesse of the resulting state (default 4).
Returns sv:	A `quantumstate.StateVector`.

Paramter func:	Function that takes a StateVector as argument.
Parameters:	svt (bool) – (optional) If svt is True, the return value will be an instance of StateVectorTrajectory.

cpypyqed Tools¶

`tools.quantumstate`¶

`tools.initialconditions`¶

Table Of Contents

Previous topic

Next topic

This Page

Navigation

cpypyqed Tools¶

tools.quantumstate¶

tools.initialconditions¶

Table Of Contents

Previous topic

Next topic

This Page

Quick search

Navigation

`tools.quantumstate`¶

`tools.initialconditions`¶