CPPQEDelements/frees/MultiLevel.h and CPPQEDelements/interactions/MLJC.h, the latter acronym standing for multi-level Jaynes-Cummings.An 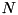 -level system is characterized by a set of basis vectors
-level system is characterized by a set of basis vectors
![\[\ket{i},\quad i=0\dots N-1\]](form_60.png)
A generic Hamiltonian with coherent driving – e.g. with laser light – between certain levels and (Jaynes-Cummings) coupling to a (driven) harmonic oscillator with ladder operator 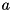 may read
may read
![\[ H=\sum_i h_i\ket i\bra i +i\sum_{\underset{\text{driven}}{i,j\in}}\lp\eta_{ij}\,e^{-i\omega_{ij}t}\ket j\bra i-\text{h.c.}\rp +i\sum_{\underset{\text{coupled}}{i,j\in}}\lp g_{ij}\,a\ket j\bra i-\text{h.c.}\rp +\omegaM\,\adagger a +i\lp\eta e^{-i\omega t}\adagger-\text{h.c.}\rp \]](form_62.png)
with 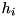 energy of level
energy of level 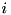 ,
, 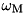 bare oscillator frequency,
bare oscillator frequency, 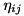 driving strength between levels
driving strength between levels 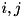 with frequency
with frequency 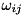 ,
, 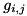 coupling strength between transition
coupling strength between transition 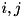 and the mode,
and the mode, 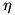 mode driving strength with frequency
mode driving strength with frequency 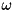 .
.
On passing to the frame rotating with 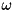 :
:
![\[ H=\sum_i h_i\ket i\bra i +i\sum_{\underset{\text{driven}}{i,j\in}}\lp\eta_{ij}\,e^{-i\omega_{ij}t}\ket j\bra i-\text{h.c.}\rp +i\sum_{\underset{\text{coupled}}{i,j\in}}\lp g_{ij}\,a\,e^{-i\omega t}\ket j\bra i-\text{h.c.}\rp -\deltaM\,\adagger a +i\lp\eta \adagger-\text{h.c.}\rp \]](form_72.png)
it becomes apparent that from the multilevel system’s point of view, the driving and coupling terms are algebraically equivalent with 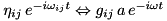 . To eliminate explicit time-dependence, we apply the unitary transformation:
. To eliminate explicit time-dependence, we apply the unitary transformation:
![\[ U=e^{-i\,t\sum_i\Omega_i\ket i\bra i} \]](form_74.png)
yielding
![\[ H=\sum_i \lp h_i-\Omega_i\rp\ket i\bra i +i\sum_{\underset{\text{driven}}{i,j\in}}\lp\eta_{ij}\,e^{i\lp\Omega_j-\Omega_i-\omega_{ij}\rp t}\ket j\bra i-\text{h.c.}\rp +i\sum_{\underset{\text{coupled}}{i,j\in}}\lp g_{ij}\,a\,e^{i\lp\Omega_j-\Omega_i-\omega\rp t}\ket j\bra i-\text{h.c.}\rp -\deltaM\,\adagger a +i\lp\eta \adagger-\text{h.c.}\rp \]](form_75.png)
So the system of equations to be solved for 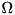 s in order to eliminate time dependence reads:
s in order to eliminate time dependence reads:
![\[\Omega_j-\Omega_i-\omega_{ij}\text{ for }i,j\in\text{set of driven transitions}\]](form_77.png)
![\[\Omega_j-\Omega_i-\omega\text{ for }i,j\in\text{set of coupled transitions}\]](form_78.png)
which can be solved in many cases of interest, especially if, as is often the case in actual experiments, all 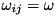 .
.
Hence we get the simplified Hamiltonian
![\[ H=-\sum_i\delta_i\ket i\bra i +i\sum_{\underset{\text{driven}}{i,j\in}}\lp\eta_{ij}\ket j\bra i-\text{h.c.}\rp +i\sum_{\underset{\text{coupled}}{i,j\in}}\lp g_{ij}\,a\ket j\bra i-\text{h.c.}\rp -\deltaM\,\adagger a +i\lp\eta \adagger-\text{h.c.}\rp \]](form_80.png)
with  .
.
This is the Hamiltonian that can be implemented by the elements in the MultiLevel bundle, in particular,
![\[J_{j\rightarrow i}=\sqrt{2\gamma_{ij}}\ket i\bra j\]](form_82.png)
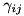 .
.
![\[-\delta_i\ket i\bra i\Longrightarrow-iz_i\ket i\bra i\text{ with }z_i=-i\delta_i+\sum_k\gamma_{ki}\]](form_84.png)
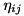 ), couplings to harmonic-oscillator modes (
), couplings to harmonic-oscillator modes ( 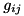 ), and decays (
), and decays ( 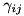 ) can be defined at compile time as lists of pairs of
) can be defined at compile time as lists of pairs of 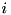 and
and 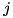 levels. From these lists, the framework assembles the Hamiltonian of the system at compile time to a form corresponding to the last one above, and the Lindblad operators as a set of operators like above. Then, the values of parameters like
levels. From these lists, the framework assembles the Hamiltonian of the system at compile time to a form corresponding to the last one above, and the Lindblad operators as a set of operators like above. Then, the values of parameters like 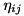 ,
, 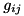 , and
, and 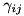 for all the pairs such defined can be specified at runtime. The rationale of this arrangement is that such pairs of levels as are never expected to be driven or coupled (or lossy), will not pollute the Hamiltonian with terms which would turn out to be zero at runtime. (Or, if the pair is not specified in the list of decays, it will not be considered when trying for quantum jumps.)
for all the pairs such defined can be specified at runtime. The rationale of this arrangement is that such pairs of levels as are never expected to be driven or coupled (or lossy), will not pollute the Hamiltonian with terms which would turn out to be zero at runtime. (Or, if the pair is not specified in the list of decays, it will not be considered when trying for quantum jumps.)In this case, three levels have increasing energy 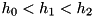 , and we have driving (or coupling to a mode or one mode each) between 0,1 and 1,2. Then, the equations can be solved for two different driving strengths. Putting
, and we have driving (or coupling to a mode or one mode each) between 0,1 and 1,2. Then, the equations can be solved for two different driving strengths. Putting 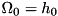 , we get
, we get 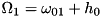 and
and 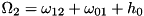 . The Hamiltonian reads:
. The Hamiltonian reads:
![\[ H=-\left[\omega_{01}-\lp h_1-h_0\rp\right]\ket 1\bra 1-\left[\omega_{01}+\omega_{12}-\lp h_2-h_0\rp\right]\ket 2\bra 2 +i\lp\eta_{01}\ket 1\bra 0-\text{h.c.}\rp+i\lp\eta_{12}\ket 2\bra 1-\text{h.c.}\rp \]](form_91.png)
In this case, three levels are ordered as 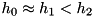 , and we have driving (or coupling to a mode or one mode each) between 0,1 and 1,2. Then, the equations can be solved for two different driving strengths. Putting
, and we have driving (or coupling to a mode or one mode each) between 0,1 and 1,2. Then, the equations can be solved for two different driving strengths. Putting 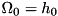 , we get
, we get 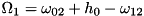 and
and 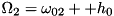 . The Hamiltonian reads:
. The Hamiltonian reads:
![\[ H=-\left[\omega_{02}-\omega_{12}-\lp h_1-h_0\rp\right]\ket 1\bra 1-\left[\omega_{02}-\lp h_2-h_0\rp\right]\ket 2\bra 2 +i\lp\eta_{02}\ket 2\bra 0-\text{h.c.}\rp+i\lp\eta_{12}\ket 2\bra 1-\text{h.c.}\rp \]](form_95.png)
In case of 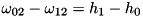 we get the Raman scheme, with only the upmost level rotating.
we get the Raman scheme, with only the upmost level rotating.
Raman.cc and CavityRaman.cc in CPPQEDscripts for actual implementations.CPPQEDscripts/Ca40InCavity.cc demonstrates more complex usage. This script represents a 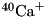 ion interacting with a cavity mode as described e.g. in Reference [1]. In this case, the
ion interacting with a cavity mode as described e.g. in Reference [1]. In this case, the 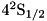 ,
, 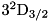 , and
, and 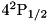 levels of the ion constitute an eight-level system, with two pumped transitions, six transitions coupled to the cavity mode, and ten decaying transitions.
levels of the ion constitute an eight-level system, with two pumped transitions, six transitions coupled to the cavity mode, and ten decaying transitions.