The MCWF method [2] [3] [4] [6] aims at the simulation of open quantum systems based on a stochastic (“Monte Carlo”) trajectory. In terms of dimensionality, this is certainly a huge advantage as compared to solving the Master equation directly. On the other hand, stochasticity requires us to run many trajectories, but the method provides an optimal sampling of the ensemble density operator so that the relative error is inversely proportional to the number of trajectories.

The optimal sampling is achieved by evolving the state vector in two steps, one deterministic and one stochastic (quantum jump). Suppose that the Master equation of the system is of the form

$\dot\rho=\frac1{i\hbar}\comm{H}\rho+\Liou\rho\equiv\frac1{i\hbar}\comm{H}\rho+\sum_m\lp J_m\rho J_m^\dag-\frac12\comm{J_m^\dag J_m}{\rho}_+\rp\equiv\frac1{i\hbar}\lp\HnH\rho-\rho\HnH^\dagger\rp+\sum_mJ_m\rho J_m^\dag.$

This is the usual form in quantum optics, and, in fact, the most general (so-called Lindblad) form. The non-Hermitian Hamiltonian is defined as

$\HnH=H-\frac{i\hbar}2\sum_m J^\dag_m J_m.$

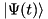At time $t$ the system is in a state with normalised state vector $\ket{\Psi(t)}$ . To obtain the state vector at time 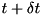$t+\delta t$ up to first order in $\delta t$ :

The state vector is evolved according to the nonunitary dynamics
$i\hbar\frac{d\ket{\Psi}}{dt}=\HnH\ket{\Psi}$
to obtain (up to first order in $\delta t$ )
$\ket{\Psi_{\text{nH}}(t+\delta t)}=\lp1-\frac{i\HnH\,\delta t}\hbar\rp \ket{\Psi(t)}.$
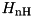Since $\HnH$ is non-Hermitian, this new state vector is not normalised. The square of its norm reads
$\braket{\Psi_{\text{nH}}(t+\delta t)}{\Psi_{\text{nH}}(t+\delta t)}=\bra{\Psi(t)}\lp1+\frac{iH^\dag_{\text{nH}}\,\delta t}\hbar\rp\lp1-\frac{i\HnH\,\delta t}\hbar\rp\ket{\Psi(t)}\equiv 1-\delta p,$
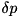where $\delta p$ reads
$\delta p=\delta t\,\frac i\hbar \bra{\Psi(t)}\HnH-H^\dag_{\text{nH}}\ket{\Psi(t)}\equiv\sum_m\delta p_m,\quad\delta p_m=\delta t\,\bra{\Psi(t)} J^\dag_m J_m\ket{\Psi(t)}\geq 0.$
Note that the timestep $\delta t$ should be small enough so that this first-order calculation be valid. In particular, we require that
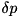$\delta p\ll1.$
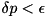A possible quantum jump with total probability $\delta p$ . For the physical interpretation of such a jump, cf. [4] [6]. We choose a random number $\epsilon$ between 0 and 1, and if $\delta p<\epsilon$ , which should mostly be the case, no jump occurs and for the new normalised state vector at 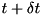$t+\delta t$ we take
$\ket{\Psi(t+\delta t)}=\frac{\ket{\Psi_{\text{nH}}(t+\delta t)}}{\sqrt{1-\delta p}}.$
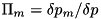If $\epsilon<\delta p$ , on the other hand, a quantum jump occurs, and the new normalised state vector is chosen from among the different state vectors $J_m\ket{\Psi(t)}$ according to the probability distribution $\Pi_m=\delta p_m/\delta p$ :
$\ket{\Psi(t+\delta t)}=\sqrt{\delta t}\frac{J_m\ket{\Psi(t)}}{\sqrt{\delta p_m}}.$

Refinement of the method

An adaptive MCWF method

The method as described above has several shortcomings. Firstly, subsequent steps of no-jump evolution (Step 1) reduce to the first order (Euler) method of evolving the Schrödinger equation, which is inappropriate in most cases of interest. Instead, to perform Step 1, we use an adaptive step-size ODE routine, usually the embedded Runge-Kutta Cash-Karp algorithm [7]. This has an intrinsic time-step management, which strives to achieve an optimal stepsize within specified (absolute and relative) error bounds.

A second problem with the original proposal is that it leaves unspecified what is to be done if after the coherent step, when calculating 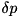$\delta p$ , we find that condition $\delta p\ll1$ is not fulfilled. (With the fixed stepsize Euler method this happens if the jump rate grows too big, but with the adaptive stepsize algorithm, it can happen also if the timestep grows too big.)

In the framework, we adopt a further heuristic in this case, introducing a tolerance interval for too big 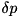$\delta p$ values: If at 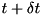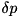$t+\delta t$ , $\delta p$ overshoots a certain 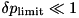$\delta p_\text{limit}\ll1$ , then from the jump rate at this time instant, a decreased stepsize is extracted to be feeded into the ODE stepper as the stepsize to try for the next timestep. On the other hand, if 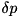$\delta p$ overshoots a 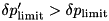$\delta p_\text{limit}'>\delta p_\text{limit}$ , then the step is altogether discarded, the state vector and the state of the ODE stepper being restored to cached states at time $t$ .

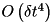Note: In spite of the RKCK method being of order $O\lp\delta t^4\rp$ , the whole method remains 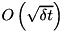$O\lp\sqrt{\delta t}\rp$ , since the treatment of jumps is essentially the same as in the original proposal. (Events of multiple jumps in one timestep are neglected.)

See also: quantumtrajectory::MCWF_Trajectory for the actual implementation

Exploiting interaction picture

In many situations it is worth using some sort of interaction picture, which means that instead of the non-Hermitian Schrödinger equation above, we strive to solve

$i\hbar\frac{d\ket{\Psi_{\text{I}}}}{dt}=U^{-1}\lp\HnH U-i\hbar\frac{dU}{dt}\rp\ket{\Psi_{\text I}},$

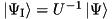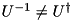where $\ket{\Psi_{\text I}}=U^{-1}\ket\Psi$ . Note that $U$ can be nonunitary, and therefore in general $U^{-1}\neq U^\dagger$ .

See also: On non-unitary transformations in quantum mechanics these notes.

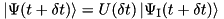The two pictures are accorded after each timestep, i.e. before the timestep $\ket{\Psi_{\text I}(t)}=\ket{\Psi(t)}$ and after the timestep, the transformation $\ket{\Psi(t+\delta t)}=U(\delta t)\ket{\Psi_{\text I}(t+\delta t)}$ is performed. 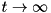This we do on one hand for convenience and for compatibility with the case when no interaction picture is used, but on the other hand also because $U(t)$ is nonunitary and hence for $t\to\infty$ some of its elements will become very large, while others very small, possibly resulting in numerical problems. It is in fact advisable to avoid evaluating $U(t)$ with very large $t$ arguments.

See also: the discussion at structure::Exact

Table of Contents

Refinement of the method

An adaptive MCWF method

Exploiting interaction picture