C++QEDCore  v2 Milestone 10
a framework for simulating open quantum dynamics – core
The multi-array concept

Table of Contents

Synopsis: The state vector as a multi-array

First, we introduce basic definitions on the algebra of composite quantum systems, that is, when the state vector of the system is an element of a Hilbert space which is the direct product of elementary Hilbert spaces (by elementary we mean that it cannot be further decomposed as a direct product of more elementary Hilbert spaces):

\[\HSpace=\bigotimes_i\HSpace_i,\quad\ket\iota\in\HSpace,\quad\ket{\iota_i}\in\HSpace_i,\quad\ket\iota=\bigotimes_i\ket{\iota_i}\equiv\ket{\iota_0,\iota_1,…}\]

The number of elementary Hilbert spaces (the number of quantum numbers of the system) is referred to throughout as the rank or arity (unary, binary, ternary, quaternary, etc.) of the system.

State-vector slices

Via an example we define state-vector slices:

\[\ket\Psi\equiv\sum_\iota\Psi_\iota\ket\iota\in\HSpace,\quad\ket{\Psi^{\avr{1,3,6,7,9}}(\iota_0,\iota_2,\iota_4,\iota_5,\iota_8,\iota_{10},…)}\equiv\sum_{\iota_1,\iota_3,\iota_6,\iota_7,\iota_9}\Psi_{\iota}\ket{\iota_1,\iota_3,\iota_6,\iota_7,\iota_9}\in\bigotimes_{i=1,3,6,7,9}\HSpace_i\]

A state-vector slice is defined by the retained index positions 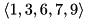$\avr{1,3,6,7,9}$, which define the subsystem, and the “dummy” indices 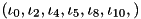$(\iota_0,\iota_2,\iota_4,\iota_5,\iota_8,\iota_{10},…)$. In situations when slicing occurs in the framework, the set of retained index positions is an information available at compile time, while the set of dummy indices is an information becoming available only at runtime.

Slicing is fully recursive in that a state-vector slice behaves exactly as a state vector, only with a lower rank. It can even be further sliced. It is in particular true that

\[\braket\iota\Psi=\braket{\iota_1,\iota_3,\iota_6,\iota_7,\iota_9}{\Psi^{\avr{1,3,6,7,9}}(\iota_0,\iota_2,\iota_4,\iota_5,\iota_8,\iota_{10},…)}\]

Via an example we define canonical operator extensions:

\[A\equiv\sum_kA_\text{k,3}\otimes A_\text{k,6}\otimes A_\text{k,1}\otimes A_\text{k,9}\otimes A_\text{k,7}\in\Lfrak\lp\HSpace_\text{3}\otimes\HSpace_\text{6}\otimes\HSpace_\text{1}\otimes\HSpace_\text{9}\otimes\HSpace_\text{7}\rp\]

\[A^{\avr{3,6,1,9,7}}(\HSpace)\equiv\sum_k\lp\idop_0\otimes A_\text{k,1}\otimes\idop_2\otimes A_\text{k,3}\otimes\idop_4\otimes\idop_5\otimes A_\text{k,6}\otimes A_\text{k,7}\otimes\idop_8\otimes A_\text{k,9}\otimes\idop_{10}…\rp\in\Lfrak(\HSpace)\]

When the numbers in the angular brackets are permutations of a sequence of ordinals, this is in fact not even an extension, only a permutation of the underlying elementary Hilbert spaces.

Matrix elements of the operator in extended Hilbert spaces can then be calculated by acting with the (possibly permutated) original operator on an appropriate vector slice:

\[\bra\iota A^{\avr{3,6,1,9,7}}(\HSpace)\ket\Psi=\bra{\iota_1,\iota_3,\iota_6,\iota_7,\iota_9}A^{\avr{1,2,0,4,3}}\ket{\Psi^{\avr{1,3,6,7,9}}(\iota_0,\iota_2,\iota_4,\iota_5,\iota_8,\iota_{10},…)}\]

The `Array` class of the Blitz++ library

Due to the abovementioned recursiveness, the state vector of a composite quantum system is most conveniently represented as a complex (dcomp) multi-array. For a definition of the multi-array concept cf. the Boost.MultiArray manual.

By virtue of its adequacy for numerics and its efficiency, we have chosen the Array class from the Blitz++ library to represent state vectors on the lowest level in the framework.

In namespace cpputils, our collection of general-purpose modules, we rely on the template alias CArray, while @ higher levels of the framework, we use the more intuitive name quantumdata::Types::StateVectorLow.

Note
A general problem with the use of Blitz++ is that the use of int, size_t, and ptrdiff_t is not consistent. In the framework we tried to use them consistently, but in Blitz only int is used in all situations like indexing, extents and even rank template parameters, so in the interaction with Blitz we could not remain consistent.