Some general-purpose elements¶

Polarizable particles in optical fields¶

Mode¶

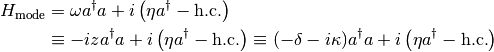
$H_\text{mode}&=\omega\adagger a+i\lp\eta\adagger-\hermConj\rp\\ &\equiv-iz\adagger a+i\lp\eta\adagger-\hermConj\rp\equiv(-\delta-i\kappa)\adagger a+i\lp\eta\adagger-\hermConj\rp$

where we have introduced

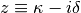
$z\equiv\kappa-i\delta$

type mode::Ptr¶

typedef boost::shared_ptr<const ModeBase> Ptr;

class Mode¶

const mode::StateVector mode::coherent(const dcomp& alpha, size_t cutoff)¶

const mode::StateVector mode::init(const mode::Pars&)¶

const mode::Ptr mode::make(const mode::Pars&, QM_Picture, const A&)¶

const mode::Ptr mode::make(const mode::ParsLossy&, QM_Picture, const A&)

const mode::Ptr mode::make(const mode::ParsPumped&, QM_Picture, const A&)

const mode::Ptr mode::make(const mode::ParsPumpedLossy&, QM_Picture, const A&): template<typename A>

Particle in momentum space¶

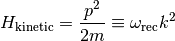
$H_\text{kinetic}=\frac{p^2}{2m}\equiv\omrec k^2$

class particle::Spatial¶

fin_¶: governs the finesse of space resolution: 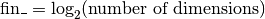$\text{fin\_}=\log_2(\text{number of dimensions})$

xMax_¶

deltaX_¶

kMax_¶

deltaK_¶

Rationale

(In the following discussion we assume 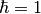$\hbar=1$ .)

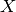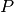Spatial is a tool to facilitate state-vector representations in both $X$ and $P$ space, where the two are canonically conjugate operators, so that 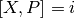$\comm{X}{P}=i$ , and hence the wave functions of two representations are linked with Fourier transformation. So for example, it can represent a single spatial degree of freedom.

Space is discretized (finite 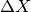$\Delta X$ ) and limited ( 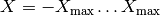$X=-X_\text{max}\dots X_\text{max}$ ), with periodic boundary condition. From discrete space, it follows that momentum is limited ( 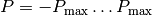$P=-P_\text{max}\dots P_\text{max}$ ), while from limited space, it follows that momentum is discretized (finite 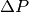$\Delta P$ ). The momentum operator is replaced by an operator 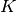$K$ with integer spectrum: 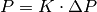$P=K\cdot\Delta P$ . When the kinetic term is expressed with this new operator 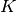$K$ , the frequency 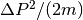$\Delta P^2/(2m)$ appears, which is called recoil frequency.

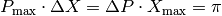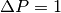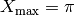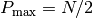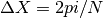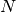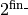From the fact that position & momentum are canonically conjugate, it follows that $P_\text{max}\cdot\Delta X=\Delta P\cdot X_\text{max}=\pi$ . In Particle and the related interactions, $\Delta P=1$ by convention. From this it follows that $X_\text{max}=\pi$ , $P_\text{max}=N/2$ and $\Delta X=2pi/N$ , where $N$ is the number of dimensions, that is, the resolution of space (equal to $2^\text{fin\_}$ ).

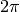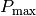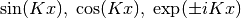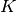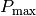When it comes to mode functions, it follows from the above that only $2\pi$ -periodic mode functions can be well represented in such a space, which do not contain Fourier components larger than $P_\text{max}$ . Therefore, for example we can represent $\sin(Kx),\;\cos(Kx),\;\exp(\pm iKx)$ with integer $K$ not larger than $P_\text{max}$ .

discuss intimacies of discrete Fourier transform...

Interactions¶

class JaynesCummings¶

class ParticleTwoModes2D¶

script: 1particle1mode¶

z cavity axis, x orthogonal direction

g pump mode function, f cavity mode function

1

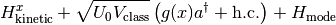
$H_\text{kinetic}^x+\sqrt{U_0\vclass}\lp g(x)\adagger+\hermConj\rp+H_\text{mode}$

2

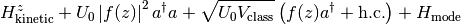
$H_\text{kinetic}^z+U_0\abs{f(z)}^2\adagger a+\sqrt{U_0\vclass}\lp f(z)\adagger+\hermConj\rp+H_\text{mode}$

3

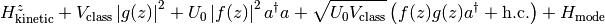
$H_\text{kinetic}^z+\vclass\abs{g(z)}^2+U_0\abs{f(z)}^2\adagger a+\sqrt{U_0\vclass}\lp f(z)g(z)\adagger+\hermConj\rp+H_\text{mode}$

4

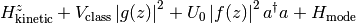
$H_\text{kinetic}^z+\vclass\abs{g(z)}^2+U_0\abs{f(z)}^2\adagger a+H_\text{mode}$

`MultiLevel`¶

class MultiLevel¶: Define multi-level systems (e.g. atoms with arbitrary level schemes) with various driving and loss schemes at compile time.

Table Of Contents

Previous topic

Next topic

Some general-purpose elements¶

Polarizable particles in optical fields¶

Mode¶

Particle in momentum space¶

Interactions¶

script: 1particle1mode¶

`MultiLevel`¶

Other¶

Navigation

Table Of Contents

Previous topic

Next topic

Quick search

Some general-purpose elements¶

Polarizable particles in optical fields¶

Mode¶

Particle in momentum space¶

Interactions¶

script: 1particle1mode¶

MultiLevel¶

Other¶

Navigation

`MultiLevel`¶