The multi-array concept¶

Synopsis: The state vector as a multi-array¶

First, we introduce basic definitions on the algebra of composite quantum systems, that is, when the state vector of the system is an element of a Hilbert space which is the direct product of elementary Hilbert spaces (by elementary we mean that it cannot be further decomposed as a direct product of more elementary Hilbert spaces):

(1) $\HSpace=\bigotimes_i\HSpace_i,\quad\ket\iota\in\HSpace,\quad\ket{\iota_i}\in\HSpace_i,\quad\ket\iota=\bigotimes_i\ket{\iota_i}\equiv\ket{\iota_0,\iota_1,…}$

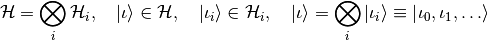
The number of elementary Hilbert spaces (the number of quantum numbers of the system) is referred to throughout as the rank or arity (unary, binary, ternary, quaternary, etc.) of the system.

Via an example we define state-vector slices:

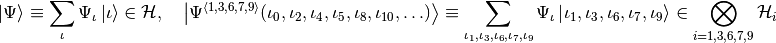
(2) $\ket\Psi\equiv\sum_\iota\Psi_\iota\ket\iota\in\HSpace,\quad\ket{\Psi^{\avr{1,3,6,7,9}}(\iota_0,\iota_2,\iota_4,\iota_5,\iota_8,\iota_{10},…)}\equiv\sum_{\iota_1,\iota_3,\iota_6,\iota_7,\iota_9}\Psi_{\iota}\ket{\iota_1,\iota_3,\iota_6,\iota_7,\iota_9}\in\bigotimes_{i=1,3,6,7,9}\HSpace_i$

A state-vector slice is defined by the retained index positions 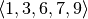$\avr{1,3,6,7,9}$ , which define the subsystem, and the “dummy” indices 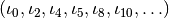$(\iota_0,\iota_2,\iota_4,\iota_5,\iota_8,\iota_{10},…)$ . In situations when slicing occurs in the framework, the set of retained index positions is an information available at compile time, while the set of dummy indices is an information becoming available only at runtime.

Slicing is fully recursive in that a state-vector slice behaves exactly as a state vector, only with a lower rank. It can even be further sliced. It is in particular true that

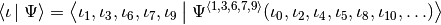
(3) $\braket\iota\Psi=\braket{\iota_1,\iota_3,\iota_6,\iota_7,\iota_9}{\Psi^{\avr{1,3,6,7,9}}(\iota_0,\iota_2,\iota_4,\iota_5,\iota_8,\iota_{10},…)}$

Via an example we define canonical operator extensions:

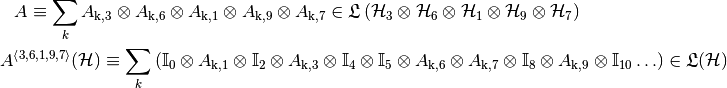
(4) $A\equiv\sum_kA_\text{k,3}\otimes A_\text{k,6}\otimes A_\text{k,1}\otimes A_\text{k,9}\otimes A_\text{k,7}\in\Lfrak\lp\HSpace_\text{3}\otimes\HSpace_\text{6}\otimes\HSpace_\text{1}\otimes\HSpace_\text{9}\otimes\HSpace_\text{7}\rp A^{\avr{3,6,1,9,7}}(\HSpace)\equiv\sum_k\lp\idop_0\otimes A_\text{k,1}\otimes\idop_2\otimes A_\text{k,3}\otimes\idop_4\otimes\idop_5\otimes A_\text{k,6}\otimes A_\text{k,7}\otimes\idop_8\otimes A_\text{k,9}\otimes\idop_{10}…\rp\in\Lfrak(\HSpace)$

When the numbers in the angular brackets are permutations of a sequence of ordinals, this is in fact not even an extension, only a permutation of the underlying elementary Hilbert spaces.

Matrix elements of the operator in extended Hilbert spaces can then be calculated by acting with the (possibly permutated) original operator on an appropriate vector slice:

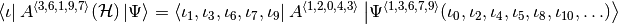
(5) $\bra\iota A^{\avr{3,6,1,9,7}}(\HSpace)\ket\Psi=\bra{\iota_1,\iota_3,\iota_6,\iota_7,\iota_9}A^{\avr{1,2,0,4,3}}\ket{\Psi^{\avr{1,3,6,7,9}}(\iota_0,\iota_2,\iota_4,\iota_5,\iota_8,\iota_{10},…)}$

The `Array` class of the Blitz++ library¶

Due to the abovementioned recursiveness, the state vector of a composite quantum system is most conveniently represented as a complex (dcomp) multi-array. For a definition of the multi-array concept cf. the Boost.MultiArray manual.

By virtue of its adequacy for numerics and its efficiency, we have chosen the Array class from the Blitz++ library to represent state vectors on the lowest level in the framework.

See also

A note on the use of Blitz++

In utils, our collection of general-purpose modules, we rely on the template alias TTD_CArray, while in higher levels of the framework we use the more intuitive name StateVectorLow.

Slice iterator and the namespace `basi`¶

The name of the namespace stands for BlitzArraySliceIterator.

Template argument definitions

int RANK

Positive integer standing for the number of elementary Hilbert spaces in (1).

typename V

Compile-time vector holding the retained index positions like 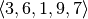$\avr{3,6,1,9,7}$ in (4).

Example models: tmptools::Vector and mpl::range_c from Boost.MPL.

mpl::size<V>::value must not be larger than RANK. V must not “contain” negative values, values not smaller than RANK, and duplicate values. These are checked for at compile time, and any violation is signalled by more or less intelligent compiler errors generated with the help of Boost.MPL’s static assertions.

bool IS_CONST

Governs the constness of Iterator.

typename A

Must be a TTD_CArray<RANK>.

class blitzplusplus::basi::Iterator¶

template <int RANK, typename V, bool IS_CONST> (cf. template parameters)

Model of ForwardIterator.

type value_type¶

This is equivalent to

TTD_CArray<RANK-mpl::size<V>::value>

when IS_CONST is false and

const TTD_CArray<RANK-mpl::size<V>::value>

when it is true. Iterator can be both const and non-const iterator depending on the last template argument.

This iterator is implemented in terms of a MultiIndexIterator, and hence it can be initialized to be either the beginning or the end of the “sequence”.

This class is at the absolute heart of the framework as it is indispensable to implement

composite quantum systems (Composite and BinarySystem)
iterations over (multi)matrix rows and columns to get (multi)vectors (cf. Iterating through rows/columns of multi-matrices)
quantumdata::ldo::DiagonalIterator

This said, it is never really used directly in the framework, but rather through the maker functions below in standard or Boost.Range algorithms.

Quite generally, by iterating through all the combinations of indeces not belonging to the given subsystem (dummy indeces) and when dereferenced returning the corresponding slice, it can be used to implement the action of operators in extended (and/or permutated) Hilbert spaces.

Semantics

Sticking to the example in (5) above, assume that the function

void actWithA(TTD_CArray<5>&);

implements the action of the operator 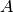$A$ on a state vector of rank 5. Then the action on the extended Hilbert space can be calculated as

void actOnExtended(TTD_CArray<11>& psi)
{
  boost::for_each(blitzplusplus::basi::fullRange(psi,
                                                 tmptools::Vector<3,6,1,9,7>()),
                  actWithA);
}

The value returned by fullRange() is a Boost.Range-compliant range, a full range of slice iterators corresponding to all the possible combinations of dummy indices (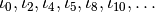 $\iota_0,\iota_2,\iota_4,\iota_5,\iota_8,\iota_{10},…$ ), and for_each is the range algorithm from Boost.Range.

For further basic examples of usage cf. C++Utils/testsuite/BlitzArraySliceIterator.cc.

Maker functions

Iterator‘s maker functions intelligently dispatch the constness of the Array:

const IterC<A, V> blitzplusplus::basi::begin(const A& array, V v)¶

const IterC<A, V> blitzplusplus::basi::end(const A& array, V v)¶

const Iter<A, V> blitzplusplus::basi::begin(A& array, V v)¶

const Iter<A, V> blitzplusplus::basi::end(A& array, V v)¶

const RangeC<A, V> blitzplusplus::basi::fullRange(const A& array, V v)¶

const Range<A, V> blitzplusplus::basi::fullRange(A& array, V v)¶

template <typename A, typename V> for all these functions (cf. template parameters)

Here, the following template aliases are in effect:

template <typename A, typename V> using IterC=Iterator<A::_bz_rank,V,true >;
template <typename A, typename V> using Iter =Iterator<A::_bz_rank,V,false>;

template <typename A, typename V> using RangeC=boost::iterator_range<IterC<A,V> >
template <typename A, typename V> using Range =boost::iterator_range<Iter <A,V> >

the trailing dummy argument V is present for allowing template-parameter deduction

The following two classes are mainly helpers for Iterator, but sometimes are used on their own as well, so they are exposed in the header file:

class blitzplusplus::basi::Transposer¶

template <int RANK, typename V> (cf. template parameters)

static TTD_CArray<RANK>& transpose(TTD_CArray<RANK>& array)¶

The returned reference simply equals the function argument.

Transposition corresponds to the “possible permutation” mentioned before Eq. (5), and is necessary in order that 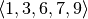$\avr{1,3,6,7,9}$ be the corresponding state vector slice, since this is how it is expected in applications. Cf. Composite for further explanations.

Semantics

static const int RANK=11;

TTD_CArray<RANK> psi;

typedef tmptools::Vector<3,6,1,9,7> Vec;
Transposer<RANK,Vec>::transpose(psi);

is equivalent to

psi.transposeSelf(0,3,2,6,4,5,1,9,8,7,10);

that is, in place of the indeces specified by the elements of the compile-time vector Vec, the elements of Vec are put, but in the order specified by Vec.

class blitzplusplus::basi::Indexer¶

template <int RANK, typename V> (cf. template parameters)

static TTD_ResCArray<V>& index(TTD_CArray<RANK>& array, TTD_ResCArray<V>& arrayRes, const TTD_VecIdxTiny<RANK, V>& idx)¶

The returned reference simply equals the second function argument.

Here the following local template aliases are in effect:

class TTD_ResCArray¶

template <typename V>:

template <typename V> using TTD_ResCArray=TTD_CArray<mpl::size<V>::value>

class TTD_VecIdxTiny¶

template <int RANK, typename V>:

template <int RANK, typename V> using TTD_VecIdxTiny=TTD_IdxTiny<RANK-mpl::size<V>::value>

Semantics

static const int RANK=11;

TTD_CArray<RANK> psi;

typedef tmptools::Vector<3,6,1,9,7> Vec;
TTD_ResCArray<VEC> psiRes;
TTD_VecIdxTiny<RANK,VEC> idxTiny;

Indexer<RANK,Vec>::index(psi,psiRes,idxTiny);

is equivalent to

const blitz::Range a(blitz::Range::all());
psiRes.reference(psi(0,a,2,a,4,5,a,a,8,a,10));

Notes on implementation¶

Some notes on the slice iterator’s implementation
- A metaprogramming example

Performance¶

As a function of the arity of slices (size of V) cf. C++Utils/testsuite/BlitzArraySliceIterator.cc 5th test case.

Table Of Contents

Previous topic

Next topic

The multi-array concept¶

Synopsis: The state vector as a multi-array¶

The `Array` class of the Blitz++ library¶

Slice iterator and the namespace `basi`¶

Notes on implementation¶

Performance¶

Navigation

Table Of Contents

Previous topic

Next topic

Quick search

The multi-array concept¶

Synopsis: The state vector as a multi-array¶

The Array class of the Blitz++ library¶

Slice iterator and the namespace basi¶

Notes on implementation¶

Performance¶

Navigation

The `Array` class of the Blitz++ library¶

Slice iterator and the namespace `basi`¶