Formalism

We adopt the so-called covariant-contravariant formalism (cf. e.g. [1]), which in physics is primarily known from the theory of relativity. Assume we have a basis 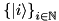$\lbr\ket{i}\rbr_{i\in\mathbb{N}}$ , where the basis vectors are non-orthogonal, so that the metric tensor

$g_{ij}\equiv\braket{i}{j}$

is nondiagonal. The contravariant components of a state vector 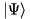$\ket\Psi$ are then defined as the expansion coefficients

$\ket\Psi\equiv\Psi^i\ket{i},$

where we have adopted the convention that there is summation for indices appearing twice. In this case one index has to be down, while the other one up, otherwise we have as it were a syntax error. This ensures that the result is independent of the choice of basis, as one would very well expect e.g. from the trace of an operator. The covariant components are the projections

$\Psi_i\equiv\braket{i}\Psi.$

The two are connected with the metric tensor:

$\Psi_i=g_{ij}\Psi^j,\quad\Psi^i=g^{ij}\Psi_j,$

where it is easy to show that 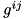$g^{ij}$ is the matrix inverse of the above defined $g_{ij}$ :

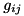$g_{ik}g^{kj}\equiv g_i^j=\delta_{ij}.$

For the representation of operators assume 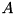$A$ is an operator, then

$\ket\Phi\equiv A\ket\Psi=\Psi^jA\ket{j},$

multiplying from the left by $\bra{i}$ yields

$\Phi_i=\bra iA\ket j\Psi^j\equiv A_{ij}\Psi^j.$

While the definition of the up-indices matrix of the operator can be read from

$\Phi=\Phi^i\ket i\equiv A^{ij}\Psi_j\ket{i}=A^{ij}\braket{j}\Psi\ket{i}=\lp A^{ij}\ket{i}\bra{j}\rp\ket\Psi=A\ket\Psi.$

Hermitian conjugation

From the above it is easy to see that

$\lp A^\dag\rp_{ij}=\lp A_{ji}\rp^*,\;\text{and}\;\lp A^\dag\rp^{ij}=\lp A^{ji}\rp^*.$

The situation, however, is more involved with the mixed-index matrices since conjugation mixes the two kinds:

${\lp A^\dag\rp_i}^j=\lp {A^j}_i\rp^*,\;\text{and}\;{\lp A^\dag\rp^i}_j=\lp {A_j}^i\rp^*.$

Here we prove the second:

${A_j}^i=A_{jk}g^{ki}=\lp\lp A^\dag\rp_{kj}\rp^*g^{ki},$

so that

$\lp{A_j}^i\rp^*=\lp A^\dag\rp_{kj}\lp g^{ki}\rp^*=g^{ik}\lp A^\dag\rp_{kj}={\lp A^\dag\rp^i}_j,$

where we have used the Hermiticity of the metric tensor.

Implications

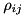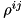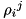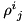If one is to apply the above formalism for density matrices in non-orthogonal bases, one has to face some strange implications: The well-known properties of Hermiticity and unit trace are split: $\rho_{ij}$ and $\rho^{ij}$ will be Hermitian matrices, but their trace is irrelevant, in fact, it is not conserved during time evolution, while ${\rho_i}^j$ and ${\rho^i}_j$ have unit conserved trace.

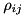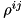This means that e.g. the quantumtrajectory::Master driver has to use either $\rho_{ij}$ or $\rho^{ij}$ (by convention, it uses the latter, which also means that quantumtrajectory::MCWF_Trajectory uses 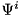$\Psi^i$ ) to be able to calculate the evolution using the real part as in Description of the Master-equation evolution (otherwise, it is not the real part which appears there). On the other hand, for all normalizations one index has to be pulled, and this (at least in the case of density operators) has to be done in place to avoid excessive copying, which also means that the index has to be pulled back again afterwards.

Table of Contents

Formalism

Hermitian conjugation

Implications