C++QEDElements  2.100.2 (v2 Milestone 10 Development branch)
a framework for simulating open quantum dynamics – generic elements
 All Classes Namespaces Files Functions Variables Typedefs Enumerations Friends Modules Pages
Table of supported general-purpose elements

Table of Contents

Abstract
This is a list of general-purpose free and interaction elements (residing in CPPQEDelements), that are supported in the framework, meaning that they will always remain an integral part of the framework’s distribution. The supported scripts (residing in CPPQEDscripts) rely on them so that they are tested by the testsuite(s). The exact list of these elements does have some historical determination and the list may be extended and supplemented in the future. For how to add custom elements to the framework and write custom scripts using them cf. the directories CustomElementsExample and CustomScriptsExample.

Frees

Reside in CPPQEDelements/frees

Mode

A single harmonic-oscillator mode that might be driven and interact with a reservoir of possibly finite temperature. Notation: $z\equiv\kappa(2n_\text{Th}+1)-i\delta$.

Class name Hamiltonian 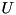$U$ Liouvillean Displayed characteristics
Mode n/a $e^{i\delta\,t\,a^\dagger a}$ n/a $\avr{a^\dagger a},\;\text{var}\lp a^\dagger a\rp,\;\real{a},\;\imag{a},$ …
ModeSch $-\delta\,a^\dagger a$ n/a ” ”
PumpedMode 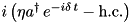$i\lp\eta a^\dagger\,e^{-i\delta\,t}-\hermConj\rp$ = Mode ” ”
PumpedModeSch 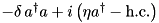$-\delta\,a^\dagger a+i\lp\eta a^\dagger-\hermConj\rp$ n/a ” ”
LossyMode n/a 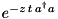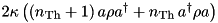$e^{-z\,t\,a^\dagger a}$ $2\kappa\lp(n_\text{Th}+1)\,a\rho a^\dagger+n_\text{Th}\,a^\dagger\rho a\rp$ ”
LossyModeUIP 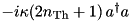$-i\kappa(2n_\text{Th}+1)\,a^\dagger a$ = Mode “ ”
LossyModeSch 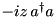$-iz\,a^\dagger a$ n/a ” ”
PumpedLossyMode 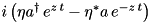$i\lp\eta a^\dagger\,e^{z\,t}-\eta^* a\,e^{-z\,t}\rp$ = LossyMode ” ”
PumpedLossyModeUIP LossyModeUIP + PumpedMode = Mode ” ”
PumpedLossyModeSch LossyModeUIP + PumpedModeSch n/a ” ”

Qbit

Qbit has the same versions as Mode, but finite temperature is not yet implemented in this case. Notation: 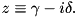$z\equiv\gamma-i\delta.$

Hamiltonian 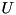$U$ Liouvillean Displayed characteristics
Qbit … 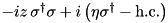$-iz\,\sigma^\dagger\sigma+i\lp\eta\sigma^\dagger-\hermConj\rp$ depends on used picture 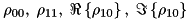$2\gamma\,\sigma\rho\sigma^\dagger$ $\rho_{00},\;\rho_{11},\;\real{\rho_{10}},\;\imag{\rho_{10}}$
Note
The Qbit algebra is identical to a Mode with cutoff=2, so that we can reuse much code from Mode when implementing Qbit

Spin

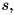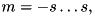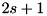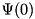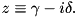
Spin is characterized by a fixed magnitude $s,$ whereupon its quantum numbers are $m=-s\dots s,$ so that its dimension is $2s+1$. In the framework, all state vectors are indexed starting with 0, so that the element $\Psi(0)$ corresponds to the basis vector $\ket{-s}$. Notation: $z\equiv\gamma-i\delta.$

Class name Hamiltonian 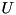$U$ Liouvillean Displayed characteristics
Spin n/a 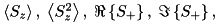$e^{-z\,t\,S_z}$ n/a $\avr{S_z},\;\avr{S_z^2},\;\real{S_+},\;\imag{S_+},$ …
LossySpin n/a ” 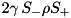$2\gamma\,S_-\rho S_+$ ”
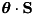SpinSch $-z\,\boldsymbol{\theta}\cdot\mathbf{S}$ n/a n/a ”
Note
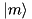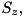$\boldsymbol{\theta}\cdot\mathbf{S}$ is in general not diagonal in the eigenbasis $\ket{m}$ of $S_z,$ so that it would not be convenient for defining an interaction picture.

Particle

These elements could be more accurately called a 1D motional degree of freedom.

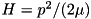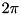The basic Hamiltonian $H=p^2/(2\mu)$ is most conveniently implemented in momentum basis. Discrete k-basis amounts to finite quantization length in x-space. Our choice of units is such that the smallest momentum is $\Delta k=1$, so that the quantisation length in x-space is $2\pi$. The use of discrete k-basis entails periodic boundary condition in x-basis. Spatial resolution is an integer power of 2 to be able to perform radix-2 FFT.

Notation: recoil frequency 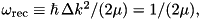$\omrec\equiv\hbar\,\Delta k^2/(2\mu)=1/(2\mu),$ k-operator 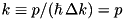$k\equiv p/(\hbar\,\Delta k)=p$. Hence the basic Hamiltonian: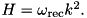 $H=\omrec k^2.$

The Particle elements have conservative dynamics.

Class name Hamiltonian 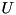$U$ Displayed characteristics
Particle n/a 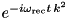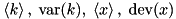$e^{-i\omrec t\,k^2}$ $\avr{k},\;\text{var}(k),\;\avr{x},\;\text{dev}(x)$ …
ParticleSch 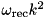$\omrec k^2$ n/a ”
PumpedParticle 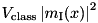$\vclass\abs{m\Int(x)}^2$ = Particle ”
PumpedParticleSch $\omrec k^2+\vclass\abs{m(x)}^2$ n/a ”

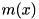Here, $m(x)$ is the mode function of the pump, which can be 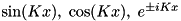$\sin(Kx),\;\cos(Kx),\;e^{\pm iKx}$ with arbitrary integer $K$.

Note
Simulation of moving particles is inherently hard, since the Schrödinger equation is a partial differential equation, and we inevitably have to deal with both position and momentum representations, which are linked by Fourier transformation. In quantum optics, however, the particles are mostly moving in potentials created by electromagnetic fields, mainly standing and running waves. In this case we can stay in momentum space during the whole time evolution. A strange consequence is that in numerical physics the harmonic oscillator seems to be hard, while the cosine potential is easy.

PumpedLossyMultiLevelSch

See also
The MultiLevel bundle

Interactions

Reside in CPPQEDelements/interactions

All the operators are automatically taken in interaction picture, if the underlying free element is in interaction picture.

Class name Free elements Hamiltonian Displayed characteristics
JaynesCummings (Qbit / Spin) – Mode 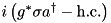$i\lp g^*\sigma a^\dagger-\hermConj\rp$ n/a
GeneralDicke Mode – Spin $\displaystyle u\,a^\dagger a\lp S_z+\frac s2\rp+y\lp a+a^\dagger\rp S_x$ n/a
NX_CoupledModes Mode – Mode 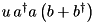$u\,a^\dagger a\lp b+b^\dagger\rp$ n/a
QbitModeCorrelations Qbit – Mode n/a 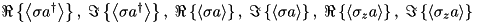$\real{\avr{\sigma a^\dagger}},\;\imag{\avr{\sigma a^\dagger}},\;\real{\avr{\sigma a}},\;\imag{\avr{\sigma a}},\;\real{\avr{\sigma_z a}},\;\imag{\avr{\sigma_z a}}$
ModeCorrelations Mode – Mode n/a covariances of the modes’ quadratures

The classes ParticleOrthogonalToCavity and ParticleAlongCavity come with several constructors which implement slightly different versions of these interactions. If passed in particlecavity::ParsAlongGenericPump or particlecavity::ParsOrthogonalGenericPump, the effective driving of the cavity 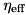$\etaeff$ is taken as parameter from this class. If passed in particlecavity::ParsAlong or particlecavity::ParsOrthogonal, the parameter 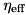$\etaeff$ is derived from the pump of the particle 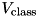$\vclass$ instead by the relation 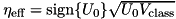$\etaeff=\text{sign}\{U_0\}\sqrt{U_0\vclass}$. In this scenario, 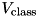$\vclass$ is either taken from the particle if it is a pumped particle, or it is passed into the constructor directly for the case of particle pump orthogonal to the particle motion.

Class name Free elements Hamiltonian Displayed characteristics
ParticleOrthogonalToCavity Mode – PumpedParticle 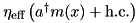$\etaeff\lp a^\dagger m(x)+\hermConj\rp$ n/a
ParticleAlongCavity Mode – Particle (pump orthogonal to cavity)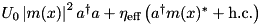$U_0\abs{m(x)}^2 a^\dagger a+\etaeff\lp a^\dagger m(x)^\ast+\hermConj\rp$ n/a
ParticleAlongCavity Mode – PumpedParticle (pump along cavity with mode function 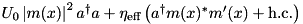$m'(x)$)$U_0\abs{m(x)}^2 a^\dagger a+\etaeff\lp a^\dagger m(x)^\ast m'(x)+\hermConj\rp$ n/a
ParticleTwoModes Mode – Mode – Particle 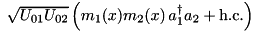$\sqrt{U_{01}U_{02}}\lp m_1(x)m_2(x)\,a_1^\dagger a_2+\hermConj\rp$ n/a
Note
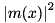In the term $\abs{m(x)}^2$, constant terms are dropped. That means this term is not present for the complex mode functions 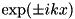$\exp(\pm ikx)$, and for 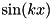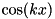$\text{sin}(kx)$ ( $\text{cos}(kx)$), this term is 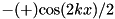$-(+)\text{cos}(2kx)/2$. The constant term can be added manually by shifting the cavity frequency accordingly, as done in the script 1particle1mode and others.

MLJC

multi-level Jaynes-Cummings

See also
The MultiLevel bundle