Abstract: This is a list of general-purpose free and interaction elements (residing in CPPQEDelements), that are supported in the framework, meaning that they will always remain an integral part of the framework’s distribution. The supported scripts (residing in CPPQEDscripts) rely on them so that they are tested by the testsuite(s). The exact list of these elements does have some historical determination and the list may be extended and supplemented in the future. For how to add custom elements to the framework and write custom scripts using them cf. the directories CustomElementsExample and CustomScriptsExample.

Frees

Reside in CPPQEDelements/frees

Mode

A single harmonic-oscillator mode that might be driven and interact with a reservoir of possibly finite temperature. Notation: 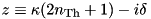$z\equiv\kappa(2n_\text{Th}+1)-i\delta$ .

Class name	Hamiltonian		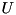Liouvillean	Displayed characteristics
Mode	n/a	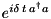$e^{i\delta\,t\,a^\dagger a}$	n/a	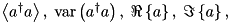$\avr{a^\dagger a},\;\text{var}\lp a^\dagger a\rp,\;\real{a},\;\imag{a},$ …
ModeSch	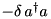$-\delta\,a^\dagger a$	n/a	”	”
PumpedMode	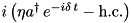$i\lp\eta a^\dagger\,e^{-i\delta\,t}-\hermConj\rp$	= Mode	”	”
PumpedModeSch	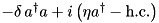$-\delta\,a^\dagger a+i\lp\eta a^\dagger-\hermConj\rp$	n/a	”	”
LossyMode	n/a	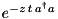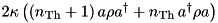$e^{-z\,t\,a^\dagger a}$	$2\kappa\lp(n_\text{Th}+1)\,a\rho a^\dagger+n_\text{Th}\,a^\dagger\rho a\rp$	”
LossyModeUIP	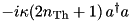$-i\kappa(2n_\text{Th}+1)\,a^\dagger a$	= Mode	“	”
LossyModeSch	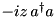$-iz\,a^\dagger a$	n/a	”	”
PumpedLossyMode	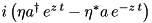$i\lp\eta a^\dagger\,e^{z\,t}-\eta^* a\,e^{-z\,t}\rp$	= LossyMode	”	”
PumpedLossyModeUIP	LossyModeUIP + PumpedMode	= Mode	”	”
PumpedLossyModeSch	LossyModeUIP + PumpedModeSch	n/a	”	”

Qbit

Qbit has the same versions as Mode, but finite temperature is not yet implemented in this case. Notation: 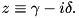$z\equiv\gamma-i\delta.$

	Hamiltonian		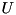Liouvillean	Displayed characteristics
Qbit …	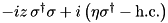$-iz\,\sigma^\dagger\sigma+i\lp\eta\sigma^\dagger-\hermConj\rp$	depends on used picture	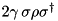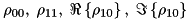$2\gamma\,\sigma\rho\sigma^\dagger$	$\rho_{00},\;\rho_{11},\;\real{\rho_{10}},\;\imag{\rho_{10}}$

Note: The Qbit algebra is identical to a Mode with cutoff=2, so that we can reuse much code from Mode when implementing Qbit

Spin

Spin is characterized by a fixed magnitude 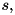$s,$ whereupon its quantum numbers are 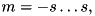$m=-s\dots s,$ so that its dimension is 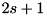$2s+1$ . In the framework, all state vectors are indexed starting with 0, so that the element 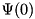$\Psi(0)$ corresponds to the basis vector 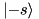$\ket{-s}$ . Notation: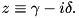 $z\equiv\gamma-i\delta.$

Class name	Hamiltonian		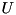Liouvillean	Displayed characteristics
Spin	n/a	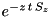$e^{-z\,t\,S_z}$	n/a	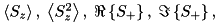$\avr{S_z},\;\avr{S_z^2},\;\real{S_+},\;\imag{S_+},$ …
LossySpin	n/a	”	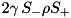$2\gamma\,S_-\rho S_+$	”
SpinSch	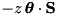$-z\,\boldsymbol{\theta}\cdot\mathbf{S}$	n/a	n/a	”

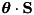Note: $\boldsymbol{\theta}\cdot\mathbf{S}$ is in general not diagonal in the eigenbasis 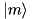$\ket{m}$ of 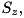so that it would not be convenient for defining an interaction picture.

Particle

These elements could be more accurately called a 1D motional degree of freedom.

The basic Hamiltonian 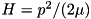$H=p^2/(2\mu)$ is most conveniently implemented in momentum basis. Discrete k-basis amounts to finite quantization length in x-space. Our choice of units is such that the smallest momentum is 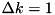$\Delta k=1$ , so that the quantisation length in x-space is 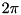$2\pi$ . The use of discrete k-basis entails periodic boundary condition in x-basis. Spatial resolution is an integer power of 2 to be able to perform radix-2 FFT.

Notation: recoil frequency 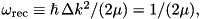$\omrec\equiv\hbar\,\Delta k^2/(2\mu)=1/(2\mu),$ k-operator 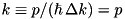$k\equiv p/(\hbar\,\Delta k)=p$ . Hence the basic Hamiltonian: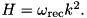 $H=\omrec k^2.$

The Particle elements have conservative dynamics.

Class name	Hamiltonian		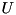Displayed characteristics
Particle	n/a	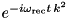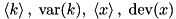$e^{-i\omrec t\,k^2}$	$\avr{k},\;\text{var}(k),\;\avr{x},\;\text{dev}(x)$ …
ParticleSch	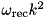$\omrec k^2$	n/a	”
PumpedParticle	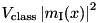$\vclass\abs{m\Int(x)}^2$	= Particle	”
PumpedParticleSch	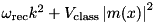$\omrec k^2+\vclass\abs{m(x)}^2$	n/a	”

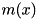Here, $m(x)$ is the mode function of the pump, which can be 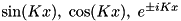$\sin(Kx),\;\cos(Kx),\;e^{\pm iKx}$ with arbitrary integer $K$ .

Note: Simulation of moving particles is inherently hard, since the Schrödinger equation is a partial differential equation, and we inevitably have to deal with both position and momentum representations, which are linked by Fourier transformation. In quantum optics, however, the particles are mostly moving in potentials created by electromagnetic fields, mainly standing and running waves. In this case we can stay in momentum space during the whole time evolution. A strange consequence is that in numerical physics the harmonic oscillator seems to be hard, while the cosine potential is easy.

PumpedLossyMultiLevelSch

See also: The MultiLevel bundle

Interactions

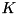Reside in CPPQEDelements/interactions

All the operators are automatically taken in interaction picture, if the underlying free element is in interaction picture.

Class name	Free elements	Hamiltonian	Displayed characteristics
JaynesCummings	(Qbit / Spin) – Mode	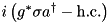$i\lp g^*\sigma a^\dagger-\hermConj\rp$	n/a
GeneralDicke	Mode – Spin	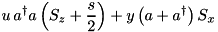$\displaystyle u\,a^\dagger a\lp S_z+\frac s2\rp+y\lp a+a^\dagger\rp S_x$	n/a
NX_CoupledModes	Mode – Mode	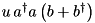$u\,a^\dagger a\lp b+b^\dagger\rp$	n/a
QbitModeCorrelations	Qbit – Mode	n/a	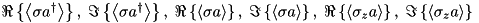$\real{\avr{\sigma a^\dagger}},\;\imag{\avr{\sigma a^\dagger}},\;\real{\avr{\sigma a}},\;\imag{\avr{\sigma a}},\;\real{\avr{\sigma_z a}},\;\imag{\avr{\sigma_z a}}$
ModeCorrelations	Mode – Mode	n/a	covariances of the modes’ quadratures
ParticleOrthogonalToCavity	Mode – PumpedParticle	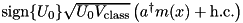$\text{sign}\{U_0\}\sqrt{U_0\vclass}\lp a^\dagger m(x)+\hermConj\rp$	n/a
ParticleAlongCavity	Mode – (Pumped)Particle	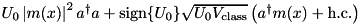$U_0\abs{m(x)}^2 a^\dagger a+\text{sign}\{U_0\}\sqrt{U_0\vclass}\lp a^\dagger m(x)+\hermConj\rp$	n/a
ParticleTwoModes	Mode – Mode – Particle	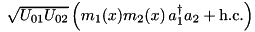$\sqrt{U_{01}U_{02}}\lp m_1(x)m_2(x)\,a_1^\dagger a_2+\hermConj\rp$	n/a

See also: This issue

MLJC

multi-level Jaynes-Cummings

See also: The MultiLevel bundle

Table of Contents