| ▼NaveragingUtils | |
| CCollecting | |
| CTransferring | |
| ▼Nmljc | |
| CBase | |
| ▼Nmode | Contains helpers for the Mode bundle |
| CAveraged | |
| CAveragedMonitorCutoff | |
| CAveragedQuadratures | |
| CExact | |
| CFockStatePreparationError_CheckYourCutoffAgainstDesiredFockState | |
| CHamiltonian | |
| CLiouvillean | |
| CLiouvillean< false, IS_ALTERNATIVE > | |
| CLiouvillean< true, IS_ALTERNATIVE > | |
| ▼Nmultilevel | Contains helpers for the MultiLevel bundle |
| CDecay | Class representing an elementary decay term (a  here) with a compile-time pair here) with a compile-time pair 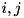 and a runtime real value and a runtime real value |
| CExact | |
| CHamiltonianIP | |
| CHamiltonianSch | |
| CLevelsMF | |
| CLiouvillean | |
| CMultiLevelExactNotImplementedException | |
| CPump | Class representing an elementary pump term (an 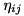 here) with a compile-time pair here) with a compile-time pair 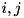 and a runtime complex value and a runtime complex value |
| CRealLevelsMF | |
| CStorage | |
| CStorage< double > | |
| ▼Nparticle | |
| CAveraged | |
| CExact | |
| CHamiltonian | |
| CInitialCondition | |
| CSpatial | |
| ▼Nqbit | |
| CAveraged | |
| CExact | |
| CHamiltonian | |
| CLiouvillean | |
| CLiouvilleanPhaseNoise | |
| ▼Nspin | |
| CPars | |
| CBIG_CLASS_NAME | |
| CCoupling | Class representing an elementary coupling term (a 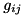 here) with a compile-time pair here) with a compile-time pair 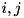 and a runtime complex value and a runtime complex value |
| CEmptyAveragingBaseForInteractions | |
| CLossyMode | Implements a mode damped with rate 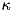 , that is , that is  , in a fully exact way, that is , in a fully exact way, that is 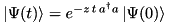 , and , and  |
| CLossyModeSch | Same as LossyMode, but in Schrödinger picture |
| CLossyModeUIP | Same as LossyMode, but in unitary interaction picture, defined only by the 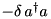 part of the Hamiltonian part of the Hamiltonian |
| CLossyQbit | |
| CLossyQbitSch | |
| CLossyQbitUIP | |
| CLossyQbitWithPhaseNoise | |
| CLossyQbitWithPhaseNoiseUIP | |
| CLossySpin | |
| CMode | Implements a free mode, that is, 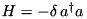 in a fully exact way, that is in a fully exact way, that is 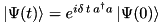 |
| CModeBase | |
| CModeSch | Same as Mode, but without exact propagation |
| CMultiLevelBase | |
| CParameterTable | Introduces ParameterTable into the global namespace to break ambiguity between update and parameters::update |
| CParticle | |
| CParticleBase | |
| CParticleSch | |
| CPumpedLossyMode | Combines LossyMode with pumping in full (non-unitary) interaction picture |
| CPumpedLossyModeAlternative | |
| CPumpedLossyModeIP_NoExact | |
| CPumpedLossyModeSch | Combines LossyModeSch and PumpedModeSch |
| CPumpedLossyModeUIP | Combines LossyModeUIP and PumpedMode |
| CPumpedLossyMultiLevelSch | Implements a free multi-level system with driving and loss |
| CPumpedLossyQbit | |
| CPumpedLossyQbitSch | |
| CPumpedLossyQbitUIP | |
| CPumpedMode | Implements a pumped mode, that is  in interaction picture defined by the first term in interaction picture defined by the first term |
| CPumpedModeSch | Same as PumpedMode, without exact propagation |
| CPumpedParticle | |
| CPumpedParticleBase | |
| CPumpedParticleSch | |
| CPumpedQbit | |
| CPumpedQbitSch | |
| CQbit | |
| CQbitBase | |
| CQbitSch | |
| CReducedDensityOperator | |
| CReducedDensityOperatorNegativity | |
| CSpin | |
| CSpinBase | |
| CSpinSch | |