Abstract: The MultiLevel bundle is a framework for representing multi-level quantum systems, e.g. atoms or ions of arbitrary level structure. Coherent driving, loss, and interaction with harmonic-oscillator modes can also be defined. The framework is defined in the header files CPPQEDelements/frees/MultiLevel.h and CPPQEDelements/interactions/MLJC.h, the latter acronym standing for multi-level Jaynes-Cummings.

Introduction

An $N$ -level system is characterized by a set of basis vectors

$\ket{i},\quad i=0\dots N-1$

A generic Hamiltonian with coherent driving – e.g. with laser light – between certain levels and (Jaynes-Cummings) coupling to a (driven) harmonic oscillator with ladder operator 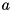$a$ may read

$H=\sum_i h_i\ket i\bra i +i\sum_{\underset{\text{driven}}{i,j\in}}\lp\eta_{ij}\,e^{-i\omega_{ij}t}\ket j\bra i-\text{h.c.}\rp +i\sum_{\underset{\text{coupled}}{i,j\in}}\lp g_{ij}\,a\ket j\bra i-\text{h.c.}\rp +\omegaM\,\adagger a +i\lp\eta e^{-i\omega t}\adagger-\text{h.c.}\rp$

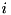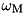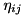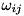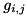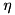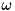with $h_i$ energy of level $i$ , $\omegaM$ bare oscillator frequency, $\eta_{ij}$ driving strength between levels $i,j$ with frequency $\omega_{ij}$ , $g_{i,j}$ coupling strength between transition $i,j$ and the mode, $\eta$ mode driving strength with frequency $\omega$ .

On passing to the frame rotating with 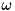$\omega$ :

$H=\sum_i h_i\ket i\bra i +i\sum_{\underset{\text{driven}}{i,j\in}}\lp\eta_{ij}\,e^{-i\omega_{ij}t}\ket j\bra i-\text{h.c.}\rp +i\sum_{\underset{\text{coupled}}{i,j\in}}\lp g_{ij}\,a\,e^{-i\omega t}\ket j\bra i-\text{h.c.}\rp -\deltaM\,\adagger a +i\lp\eta \adagger-\text{h.c.}\rp$

it becomes apparent that from the multilevel system’s point of view, the driving and coupling terms are algebraically equivalent with 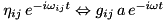$\eta_{ij}\,e^{-i\omega_{ij}t}\Leftrightarrow g_{ij}\,a\,e^{-i\omega t}$ . To eliminate explicit time-dependence, we apply the unitary transformation:

$U=e^{-i\,t\sum_i\Omega_i\ket i\bra i}$

yielding

$H=\sum_i \lp h_i-\Omega_i\rp\ket i\bra i +i\sum_{\underset{\text{driven}}{i,j\in}}\lp\eta_{ij}\,e^{i\lp\Omega_j-\Omega_i-\omega_{ij}\rp t}\ket j\bra i-\text{h.c.}\rp +i\sum_{\underset{\text{coupled}}{i,j\in}}\lp g_{ij}\,a\,e^{i\lp\Omega_j-\Omega_i-\omega\rp t}\ket j\bra i-\text{h.c.}\rp -\deltaM\,\adagger a +i\lp\eta \adagger-\text{h.c.}\rp$

So the system of equations to be solved for 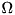$\Omega$ s in order to eliminate time dependence reads:

$\Omega_j-\Omega_i-\omega_{ij}\text{ for }i,j\in\text{set of driven transitions}$

$\Omega_j-\Omega_i-\omega\text{ for }i,j\in\text{set of coupled transitions}$

which can be solved in many cases of interest, especially if, as is often the case in actual experiments, all 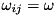$\omega_{ij}=\omega$ .

The actual Hamiltonian

Hence we get the simplified Hamiltonian

$H=-\sum_i\delta_i\ket i\bra i +i\sum_{\underset{\text{driven}}{i,j\in}}\lp\eta_{ij}\ket j\bra i-\text{h.c.}\rp +i\sum_{\underset{\text{coupled}}{i,j\in}}\lp g_{ij}\,a\ket j\bra i-\text{h.c.}\rp -\deltaM\,\adagger a +i\lp\eta \adagger-\text{h.c.}\rp$

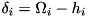with $\delta_i=\Omega_i-h_i$ .

The elements

This is the Hamiltonian that can be implemented by the elements in the MultiLevel bundle, in particular,

PumpedLossyMultiLevelSch (with corresponding maker function multilevel::makePumpedLossySch) implements the first two terms, and adds noise with jump operator
$J_{j\rightarrow i}=\sqrt{2\gamma_{ij}}\ket i\bra j$
corresponding to a single radiative transition between two levels with decay rate $\gamma_{ij}$ .
Note
In case of noise the free part of the Hamiltonian becomes non-Hermitian according to the MCWF method, to wit
$-\delta_i\ket i\bra i\Longrightarrow-iz_i\ket i\bra i\text{ with }z_i=-i\delta_i+\sum_k\gamma_{ki}$
MLJC implements the third term.

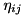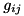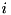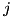Note: The bundle is designed in such a way that a set of drivings ( $\eta_{ij}$ ), couplings to harmonic-oscillator modes ( $g_{ij}$ ), and decays ( $\gamma_{ij}$ ) can be defined at compile time as lists of pairs of and levels. From these lists, the framework assembles the Hamiltonian of the system at compile time to a form corresponding to the last one above, and the Lindblad operators as a set of operators like above. 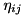Then, the values of parameters like $\eta_{ij}$ , $g_{ij}$ , and $\gamma_{ij}$ for all the pairs such defined can be specified at runtime. The rationale of this arrangement is that such pairs of levels as are never expected to be driven or coupled (or lossy), will not pollute the Hamiltonian with terms which would turn out to be zero at runtime. (Or, if the pair is not specified in the list of decays, it will not be considered when trying for quantum jumps.)

Todo:: Describe phase noise.

Examples

Ladder system

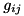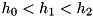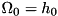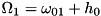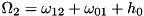In this case, three levels have increasing energy $h_0<h_1<h_2$ , and we have driving (or coupling to a mode or one mode each) between 0,1 and 1,2. Then, the equations can be solved for two different driving strengths. Putting $\Omega_0=h_0$ , we get $\Omega_1=\omega_{01}+h_0$ and $\Omega_2=\omega_{12}+\omega_{01}+h_0$ . The Hamiltonian reads:

$H=-\left[\omega_{01}-\lp h_1-h_0\rp\right]\ket 1\bra 1-\left[\omega_{01}+\omega_{12}-\lp h_2-h_0\rp\right]\ket 2\bra 2 +i\lp\eta_{01}\ket 1\bra 0-\text{h.c.}\rp+i\lp\eta_{12}\ket 2\bra 1-\text{h.c.}\rp$

Lambda system

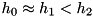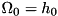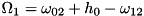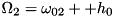In this case, three levels are ordered as $h_0\approx h_1<h_2$ , and we have driving (or coupling to a mode or one mode each) between 0,1 and 1,2. Then, the equations can be solved for two different driving strengths. Putting $\Omega_0=h_0$ , we get $\Omega_1=\omega_{02}+h_0-\omega_{12}$ and $\Omega_2=\omega_{02}++h_0$ . The Hamiltonian reads:

$H=-\left[\omega_{02}-\omega_{12}-\lp h_1-h_0\rp\right]\ket 1\bra 1-\left[\omega_{02}-\lp h_2-h_0\rp\right]\ket 2\bra 2 +i\lp\eta_{02}\ket 2\bra 0-\text{h.c.}\rp+i\lp\eta_{12}\ket 2\bra 1-\text{h.c.}\rp$

In case of $\omega_{02}-\omega_{12}=h_1-h_0$ we get the Raman scheme, with only the upmost level rotating.

Example scripts

Cf. Raman.cc and CavityRaman.cc in CPPQEDscripts for actual implementations.
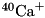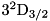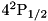The script CPPQEDscripts/Ca40InCavity.cc demonstrates more complex usage. This script represents a $^{40}\text{Ca}^{+}$ ion interacting with a cavity mode as described e.g. in Reference [1]. In this case, the $4^{2}\text S_{1/2}$ , $3^{2}\text D_{3/2}$ , and $4^{2}\text P_{1/2}$ levels of the ion constitute an eight-level system, with two pumped transitions, six transitions coupled to the cavity mode, and ten decaying transitions.

Table of Contents