Table Of Contents
Previous topic
Next topic
Quick search
Enter search terms or a module, class or function name.
The MCWF method cite{carmichael87,dalibard92,dum92,molmer93} aims at the simulation of open quantum systems based on a stochastic (“Monte Carlo”) trajectory. In terms of dimensionality, this is certainly a huge advantage as compared to solving the Master equation directly. On the other hand, stochasticity requires us to run many trajectories, but the method provides an optimal sampling of the ensemble density operator so that the relative error is inversely proportional to the number of trajectories.
The optimal sampling is achieved by evolving the state vector in two steps, one deterministic and one stochastic (quantum jump). Suppose that the Master equation of the system is of the form
(1)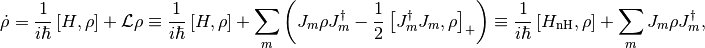
the usual form in quantum optics, and, in fact, the most general (so-called Lindblad) form. The non-Hermitian Hamiltonian is defined as
(2)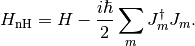
At time 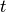 the system is in a state with normalised state vector
the system is in a state with normalised state vector 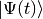 . To obtain the state vector at time
. To obtain the state vector at time 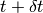 up to first order in
up to first order in 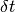 :
:
The state vector is evolved according to the nonunitary dynamics
(3)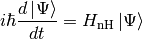
to obtain (up to first order in 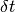 )
)
(4)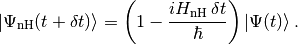
Since 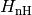 is non-Hermitian, this new state vector is not normalised. The square of its norm reads
is non-Hermitian, this new state vector is not normalised. The square of its norm reads
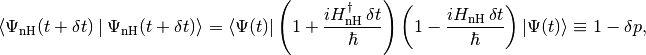
where 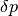 reads
reads
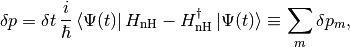
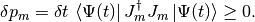
Note that the timestep  should be small enough so that this first-order calculation be valid. In particular, we require that
should be small enough so that this first-order calculation be valid. In particular, we require that
(5)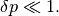
A possible quantum jump with total probability 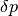 . For the physical interpretation of such a jump see e.g. Refs.citep{dum92,molmer93}. We choose a random number
. For the physical interpretation of such a jump see e.g. Refs.citep{dum92,molmer93}. We choose a random number  between 0 and 1, and if
between 0 and 1, and if 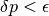 , which should mostly be the case, no jump occurs and for the new normalised state vector at
, which should mostly be the case, no jump occurs and for the new normalised state vector at 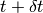 we take
we take
(6)
If
, on the other hand, a quantum jump occurs, and the new normalised state vector is chosen from among the different state vectors
according to the probability distribution
:
The method as described above has several shortcomings. Firstly, subsequent steps of no-jump evolution (Step 1) reduce to the first order (Euler) method of evolving the Schrödinger equation, which is inappropriate in most cases of interest. Instead, to perform Step 1, we use an adaptive step-size ODE routine, usually the embedded Runge-Kutta Cash-Karp algorithm cite{numrec}. This has an intrinsic time-step management, which strives to achieve an optimal stepsize within specified (absolute and relative) error bounds.
A second problem with the original proposal is that it leaves unspecified what is to be done if after the coherent step, when calculating 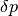 , we find that condition (5) is not fulfilled. (With the fixed stepsize Euler method this happens if the jump rate grows too big, but with the adaptive stepsize algorithm, it can happen also if the timestep grows too big.)
, we find that condition (5) is not fulfilled. (With the fixed stepsize Euler method this happens if the jump rate grows too big, but with the adaptive stepsize algorithm, it can happen also if the timestep grows too big.)
In the framework, we adopt a further heuristic in this case, introducing a tolerance interval for too big 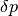 values: If at
values: If at 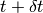 ,
, 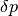 overshoots a certain
overshoots a certain 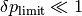 , then from the jump rate at this time instant, a decreased stepsize is extracted to be feeded into the ODE stepper as the stepsize to try for the next timestep. On the other hand, if
, then from the jump rate at this time instant, a decreased stepsize is extracted to be feeded into the ODE stepper as the stepsize to try for the next timestep. On the other hand, if 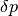 overshoots a
overshoots a 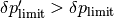 , then the step is altogether discarded, the state vector and the state of the ODE stepper being restored to cached states at time
, then the step is altogether discarded, the state vector and the state of the ODE stepper being restored to cached states at time 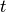 .
.
Note
In spite of the RKCK method being of order 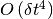 , the whole method remains
, the whole method remains 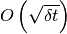 , since the treatment of jumps is essentially the same as in the original proposal. (Events of multiple jumps in one timestep are neglected.)
, since the treatment of jumps is essentially the same as in the original proposal. (Events of multiple jumps in one timestep are neglected.)
See also
For the implementation MCWF trajectory.
In many situations it is worth using some sort of interaction picture, which means that instead of Eq. (3) we strive to solve
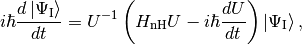
where 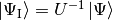 . Note that
. Note that 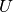 can be nonunitary, and therefore in general
can be nonunitary, and therefore in general 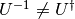 .
.
See also
On non-unitary transformations in quantum mechanics these notes.
The two pictures are accorded after each timestep, i.e. before the timestep 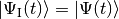 and after the timestep the transformation
and after the timestep the transformation 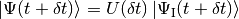 is performed. This we do on one hand for convenience and for compatibility with the case when no interaction picture is used, but on the other hand also because
is performed. This we do on one hand for convenience and for compatibility with the case when no interaction picture is used, but on the other hand also because 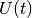 is nonunitary and hence for
is nonunitary and hence for 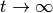 some of its elements will become very large, while others very small, possibly resulting in numerical problems. It is in fact advisable to avoid evaluating
some of its elements will become very large, while others very small, possibly resulting in numerical problems. It is in fact advisable to avoid evaluating 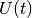 with very large
with very large 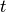 arguments.
arguments.
Cf. also the discussion at Exact.
We adopt the so-called covariant-contravariant formalism (see also cite{artacho91}), which in physics is primarily known from the theory of relativity. Assume we have a basis 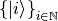 , where the basis vectors are nonorthogonal, so that the metric tensor
, where the basis vectors are nonorthogonal, so that the metric tensor
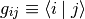
is nondiagonal. The contravariant components of a state vector 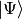 are then defined as the expansion coefficients
are then defined as the expansion coefficients
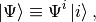
where we have adopted the convention that there is summation for indeces appearing twice. In this case one index has to be down, while the other one up, otherwise we have as it were a syntax error. This ensures that the result is independent of the choice of basis, as one would very well expect e.g. from the trace of an operator. The covariant components are the projections
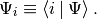
The two are connected with the metric tensor:
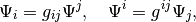
where it is easy to show that 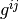 is the matrix inverse of the above defined
is the matrix inverse of the above defined 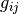 :
:
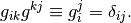
For the representation of operators assume 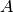 is an operator, then
is an operator, then
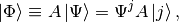
multiplying from the left by 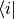 yields
yields
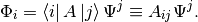
While the definition of the up-indeces matrix of the operator can be read from
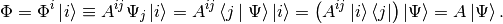
From the above it is easy to see that
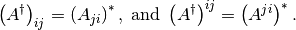
The situation, however, is more involved with the mixed-index matrices since conjugation mixes the two kinds:
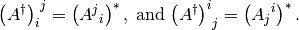
Here we prove the second:
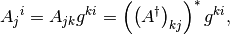
so that
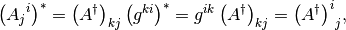
where we have used the Hermiticity of the metric tensor.
If one is to apply the above formalism for density matrices in nonorthogonal bases, one has to face some strange implications: The well-known properties of Hermiticity and unit trace are split: 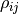 and
and 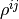 will be Hermitian matrices, but their trace is irrelevant, in fact, it is not conserved during time evolution, while
will be Hermitian matrices, but their trace is irrelevant, in fact, it is not conserved during time evolution, while 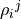 and
and 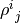 have unit conserved trace.
have unit conserved trace.
This means that e.g. the quantumtrajectory::Master driver has to use either 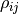 or
or 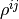 (by convention, it uses the latter, which also means that quantumtrajectory::MCWF_Trajectory uses
(by convention, it uses the latter, which also means that quantumtrajectory::MCWF_Trajectory uses 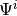 ) to be able to calculate the evolution using the real part as in Eqref{eq:Master-MCWF} (otherwise, it is not the real part which appears there). On the other hand, for all normalizations one index has to be pulled, and this (at least in the case of density operators) has to be done in place to avoid excessive copying, which also means that the index has to be pulled back again afterwards.
) to be able to calculate the evolution using the real part as in Eqref{eq:Master-MCWF} (otherwise, it is not the real part which appears there). On the other hand, for all normalizations one index has to be pulled, and this (at least in the case of density operators) has to be done in place to avoid excessive copying, which also means that the index has to be pulled back again afterwards.
The situation is even more delicate if one wants to calculate averages or jump probabilities for a subsystem. Then, as explained in Sref{sec:Jump} and Sref{sec:Displayed}, the partial density operator has to be used. Imagine that we want to calculate the expectation value of an operator 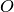 acting on a given subsystem. Imagine that we are using an MCWF trajectory, so that we dispose of the expansion coefficients
acting on a given subsystem. Imagine that we are using an MCWF trajectory, so that we dispose of the expansion coefficients 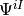 , where
, where 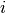 is the index (quantum number) for the given subsystem, while
is the index (quantum number) for the given subsystem, while 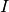 is a multi-index, fusing the (dummy) indeces of the other subsystems, which are all up. Now the matrix of partial density operator of the given subsystem reads
is a multi-index, fusing the (dummy) indeces of the other subsystems, which are all up. Now the matrix of partial density operator of the given subsystem reads
begin{equation} label{eq:NO_PartialTrace} rho^{ij}=lp{Psi^i}_Irp^*Psi^{jI}, end{equation}
and then, since we dispose of 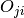 (this is most easily obtained, since only scalar products have to be calculated), the desired expectation value is obtained as
(this is most easily obtained, since only scalar products have to be calculated), the desired expectation value is obtained as
begin{equation} avr O=rho^{ij}O_{ji}. end{equation}
This means that somehow all the indeces but the index of the given subsystem have to be pulled. Then, when we move to the next subsystem (this is what code{Composite}’s code{Display} does cf Sref{sec:Composite}) to calculate the expectation value of one of its operators, we have to pull up again its index, and pull down the index of the previous subsystem, and so on. This is tedious, and possibly also wasteful.
What happens in practice is that the code{MCWF_Trajectory} driver, when it comes to display, pulls emph{all indeces} by calling the function code{Pull} for the complete code{NonOrthogonal}, and passes both the covariant and contravariant vectors to code{Display}. The summation in Eqref{eq:NO_PartialTrace} is then performed by code{ElementDisplay}, while the code{Average} of the given subsystem works with 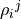 (check definition!!!!!!) to calculate
(check definition!!!!!!) to calculate 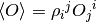 , so that the additional pull has to be implemented here on
, so that the additional pull has to be implemented here on 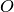 . The same procedure is repeated with code{Jump}, since to obtain the jump probability, also an expectation value has to be calculated. The drivers code{Master} and code{EnsembleMCWF} working with density operators
. The same procedure is repeated with code{Jump}, since to obtain the jump probability, also an expectation value has to be calculated. The drivers code{Master} and code{EnsembleMCWF} working with density operators 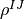 pull one (multi-)index in place to obtain
pull one (multi-)index in place to obtain 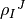 , passes this for display, and afterwards pull the index back again.
, passes this for display, and afterwards pull the index back again.
A given subsystem’s code{Average} function can therefore receive four possible sets of parameters:
begin{enumerate}
item for orthogonal basis and state-vector evolution only a single
array of code{double}s, representing 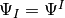 .
item for nonorthogonal basis and state-vector evolution two arrays,
representing
.
item for nonorthogonal basis and state-vector evolution two arrays,
representing 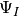 and
and 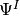 separately.
item for orthogonal basis and density-operator evolution a single
array, representing the matrix of
separately.
item for orthogonal basis and density-operator evolution a single
array, representing the matrix of 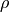 .
item for nonorthogonal basis and density-operator evolution a single
array, representing
.
item for nonorthogonal basis and density-operator evolution a single
array, representing 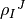 .
end{enumerate}
.
end{enumerate}
However, an actual implementor of such a function does not see the difference between these cases, since as explained in Chref{chap:Indexing}, they are hidden behind the code{Indexing} interface, an abstract class, which is then implemented to cover the four separate cases. In fact, if the given subsystem is represented in an orthogonal basis, it does not really have to know about the existence of nonorthogonal bases, the only thing which may come as a surprise is that the diagonal elements of 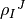 are in general not real. This is why the diagonal function of code{Indexing} returns complex...
are in general not real. This is why the diagonal function of code{Indexing} returns complex...
For reference we finally list the Master equation for 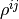 :
:
The Schr”odinger equation is:
begin{equation}
label{eq:SchEq}
ihbarfrac{dketPsi}{dt}=HketPsi.
end{equation}
It may sound strange to call this a convention, but the position
of 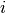 emph{is} conventional in this equation. Of course, it has to
be consistent with other postulates, in particular the canonical
commutation relations, e.g.
begin{equation}
comm xp=ihbar.
end{equation}
The consistency of these two equations can be seen e.g. from Ehrenfest’s
theorem.
emph{is} conventional in this equation. Of course, it has to
be consistent with other postulates, in particular the canonical
commutation relations, e.g.
begin{equation}
comm xp=ihbar.
end{equation}
The consistency of these two equations can be seen e.g. from Ehrenfest’s
theorem.
newcommandHinter{H^{text{int}}} newcommandIAP[1]{{#1_{text{I}}}}
From Eqref{eq:SchEq} we can derive the necessary definitions for
interaction picture. If the Hamiltonian is of the form
begin{equation}
Hequiv H^{(0)}+Hinter,
end{equation}
where 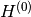 is something we can solve, then the operator
is something we can solve, then the operator 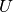 transforming between Schr”odinger picture and the interaction picture
defined by
transforming between Schr”odinger picture and the interaction picture
defined by 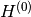 begin{equation}
ketPsiequiv U(t)ket{IAPPsi}
end{equation}
reads
begin{equation}
U(t)=e^{-frac ihbar H^{(0)} t}.
end{equation}
The Schr”odinger equation reads
begin{equation}
label{eq:SchEqIAP}
ihbarfrac{dket{IAPPsi}}{dt}=U^{-1}(t)Hinter U(t)ket{IAPPsi}
equivIAPHinter.
end{equation}
If
begin{equation}
ketPsiequiv U(t)ket{IAPPsi}
end{equation}
reads
begin{equation}
U(t)=e^{-frac ihbar H^{(0)} t}.
end{equation}
The Schr”odinger equation reads
begin{equation}
label{eq:SchEqIAP}
ihbarfrac{dket{IAPPsi}}{dt}=U^{-1}(t)Hinter U(t)ket{IAPPsi}
equivIAPHinter.
end{equation}
If  is an operator then in interaction picture it
evolves as
begin{equation}
frac{dIAP{mathcal O}}{dt}=
frac ihbarcomm{H^{(0)}}{IAP{mathcal O}}+
U^{-1}(t)frac{partialmathcal O}{partial t}U(t)
end{equation}
is an operator then in interaction picture it
evolves as
begin{equation}
frac{dIAP{mathcal O}}{dt}=
frac ihbarcomm{H^{(0)}}{IAP{mathcal O}}+
U^{-1}(t)frac{partialmathcal O}{partial t}U(t)
end{equation}
For p look at how Sakurai does