Navigation

Table Of Contents

Previous topic

Implementing a harmonic-oscillator mode

Next topic

Composites

The quantumtrajectory namespace

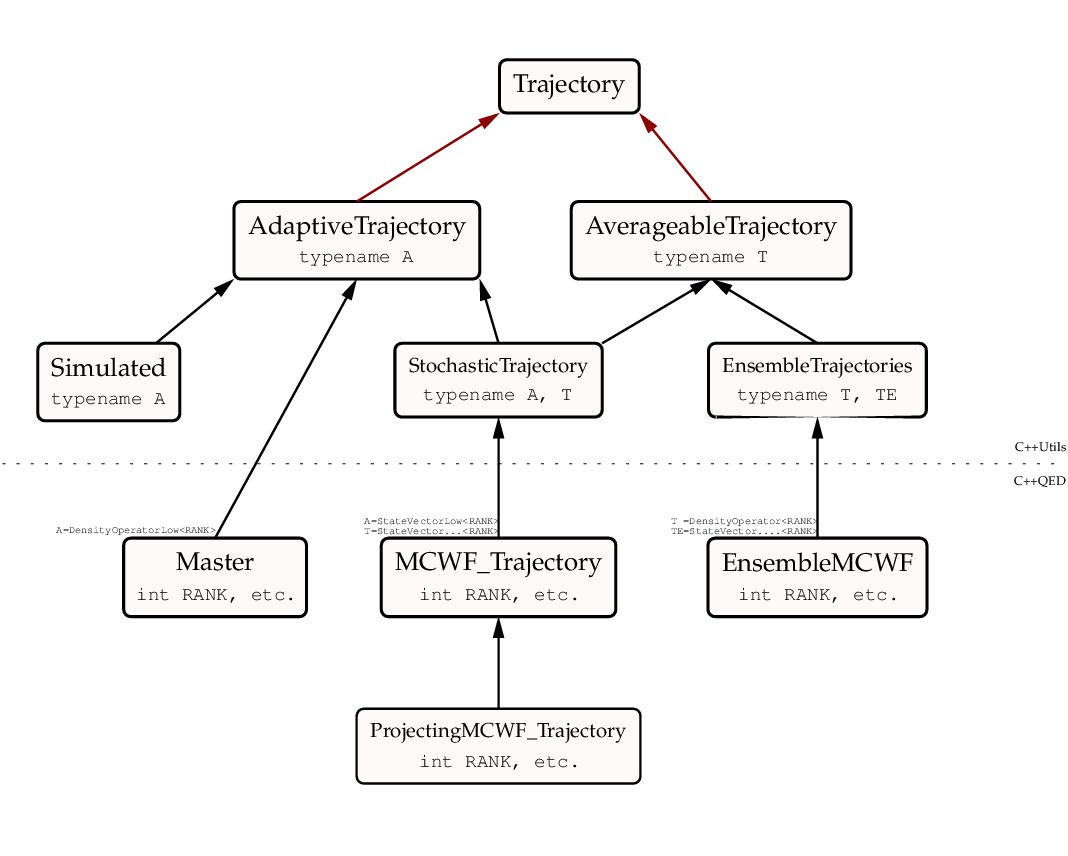
_images/trajectory.png

MCWF trajectory

In the framework, a single Monte-Carlo wave function step at time 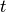t (at which point the Schrödinger- and interaction pictures coincide) is implemented as a sequence of the following stages:

  1. Coherent time development is applied:
  1. If the system time evolution has Hamiltonian part, it is evolved with an adaptive-size step (cf. Evolved). This takes the system into t+\Delta t.
  2. The exact part (if any) of the time evolution is applied, making that the Schrödinger and interaction pictures coincide again at t+\Delta t.
  3. The state vector is renormalized.
  1. If the system is not Liouvillean, the timestep ends here, reducing to a simple ODE evolution. Otherwise:
  1. The rates (probabilities per unit time) corresponding to all jump operators are calculated. If some rates are found negative (“special jump”, cf. explanation at probabilities()), then J_\text{at}\ket\Psi is calculated (and tabulated) instead, and the probability is calculated as \delta r_\text{at}=\norm{J_\text{at}\ket\Psi}^2.
  2. First, it is verified whether the total jump probability is not too big. This is performed on two levels:
  1. The total jump rate \delta r is calculated.
  2. If \delta r\delta t>\delta p_\text{limit}', the step is retraced: both the state vector and the state of the ODE stepper are restored to cached values at the beginning of the timestep, and phase I. is performed anew with a smaller stepsize \delta p_\text{limit}/\delta r. With this, we ensure that \delta p_\text{limit} is likely not to be overshot in the next try.

Note

It is assumed that \delta p_\text{limit}'>\delta p_\text{limit}, their ratio being a parameter of the MCWF stepper.

  1. If just \delta r\delta t_\text{next}>\delta p_\text{limit} (where \Delta t_\text{next} is a guess for the next timestep given by the ODE stepper), the coherent step is accepted, but the timestep to try next is modified, to reduce the likeliness of overshoot: \delta t_\text{next}\longrightarrow\delta p_\text{limit}/\delta r.

See also

The discussion at An adaptive MCWF method.

  1. After a successful coherent step resulting in an acceptable \delta r, the possible occurence of a quantum jump is considered: It is randomly decided which (if any) of the jumps to perform. If it is found to be a special jump, then the tabulated J_\text{at}\ket\Psi is taken.

Note

In phase II.2.b., another approach would be not to trace back the whole step, but make a coherent step backwards to an intermediate time instant found by linear interpolation. This has several drawbacks, however, the most significant being that in the ODE stepper, it is not clear what to take as the timestep to try at the point when the direction of time is reversed. (Although in Evolved it is simply taken to be the timestep done in the last step…)

class quantumtrajectory::MCWF_Trajectory

template <RANK>

void step(double deltaT) const

Ensembles of trajectories

class quantumtrajectory::EnsembleMCWF

...

Master equation evolution

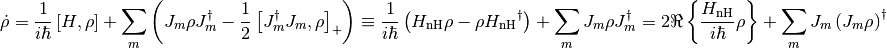
(1)\dot\rho=\frac1{i\hbar}\comm{H}{\rho}+\sum_m\lp{J_m\rho{J_m^\dag}-\frac12\comm{J_m^\dag J_m}{\rho}_+}\rp\equiv\frac1{i\hbar}\lp\HnH\rho-\rho\HnH^\dag\rp+\sum_mJ_m\rho{J_m^\dag}=2\Re\lbr\frac\HnH{i\hbar}\rho\rbr+\sum_mJ_m\lp{J_m\rho}\rp^\dag

class quantumtrajectory::Master

...

Alternative Liouvillean calculation based on additional virtual function signalled by something.

On the basis of Pictures.pdf find out when exactly the code reusal for the calculation of the Liouvillean can be applied.

Performance profile

./release/1particle1mode –evol master –dc 1 –T 1 –fin 7

operation n/timestep time
Hamiltonian (nRejected+1)*5 1.31s
TwoTimesRealPartOfSelf “ 0.05s
Liouvillean (”)*nJump 0.33s
Exact 1 0.40s
Smoothing 1 0.10s
Averaging ≤1 0.04s

Dispatcher

evolve(quantumdata::StateVector<RANK>& psi, const structure::QuantumSystem<RANK>& sys, const ParsEvolution& pe)

template<typename V, int RANK>

Navigation

© Copyright 2009, András Vukics.