namespace structure
The structure namespace comprises modules for describing quantum systems. Among them the most important is QuantumSystem, which is an abstract interface every system has to provide to be usable with quantum trajectories like MCWF_Trajectory or Master. This is why all the elementary and composite systems are more or less directly derived from QuantumSystem.
Much of the design here depends on the requirements of a step of the Monte-Carlo wave function method, as described in Sec. MCWF trajectory, so the reader is asked to have a look at there, too.
Most of the classes in this namespace belong to a single hierarchy, sketched in the following diagram (the broken lines signifying that the inheritance is not direct, due to some classes in between, which can be considered implementation details). [1]
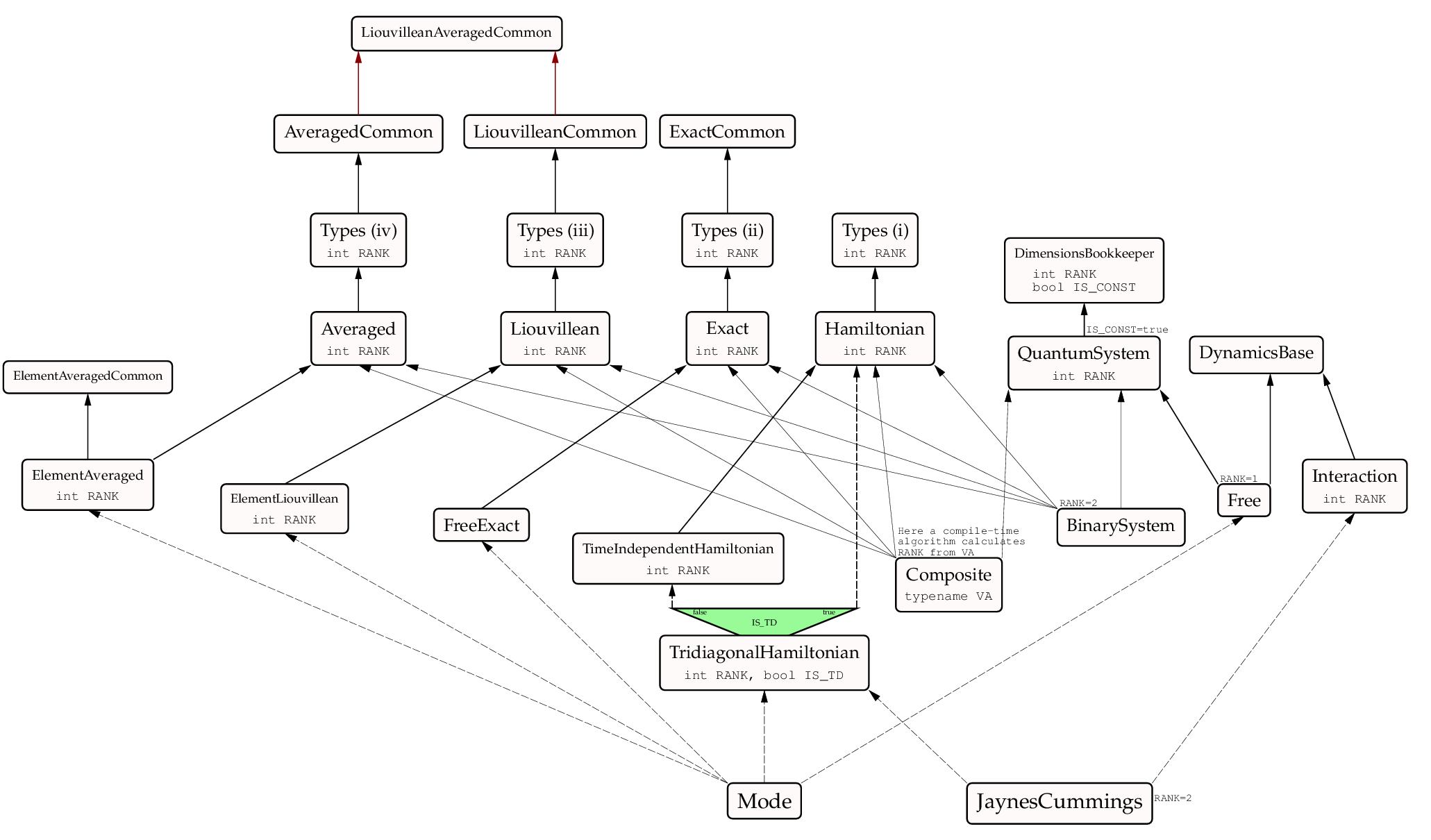
We have also indicated how elements like Mode and JaynesCummings, and composite systems as BinarySystem and Composite fit into the hierarchy.
These modules provide a lot of services for implementing new elements in the framework. For examples on how to optimally use these services, cf. the structure-bundle guide below.
Template argument definitions
DynamicsBase provides services for dealing with frequency-like parameters, both real and constant, for all elements, frees and interactions alike, which are hence all derived from this class. Such parameters need a special treatment because all such parameters from all the subsystems (either frees or interactions) of the given physical system have to be considered as the largest frequency of the system. This largest frequency is needed for determining the initial time-step of the ODE routine.
On the other hand, these parameters (together with all others) have to be communicated towards the user when the framework summarizes the parameters of a given run. Therefore, for each such parameter, the class stores not only the value, but also the name of the parameter, plus another real number which multiplies the value of the named frequency, to give the actual frequency as appearing in the ODE. An example will make this clear. Consider the Hamiltonian of a free mode:
In this case the parameter supplied by the user is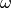 
, but the largest frequency appearing in the ODE is actually this times the dimension of the system (the cutoff of the Fock space). Hence, the tuple stored by the class for this particular frequency-like parameter will be something like:
"omega",omega,cutoff
In the case of a pumping term:
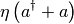
the multiplier will be different:
"eta",eta,sqrt(cutoff)
The class also stores an std::stringstream object, on which the constructor of any client (derived element class) can write its parameters, and these will in turn be displayed when displayParameters() is called for the system. Cf. tutorial above.
This is a standard list storing the name-value-multiplier tuples (cf. Boost.Tuple) for real frequency-like parameters:
typedef std::list<boost::tuple<std::string,double,double> > RealFreqs;
The same for complex:
typedef std::list<boost::tuple<std::string,dcomp,double> > ComplexFreqs;
The constructor simply expects initializers for the lists. In practice, these are usually created with the tuple_list_of function from Boost.Assignment
Calculates the fastest timescale of the given element by simply taking the maximum value*multiplier value from the lists.
Displaying parameters of the system in two steps:
Simple query functions allowing for printing on paramsStream_ and append to the list of frequencies
Virtual. The default implementation is simply printing # name=value from the lists.
(private) data member
template <int RANK> (cf. template parameters); inherits publicly from DimensionsBookkeeper
This class describes an entity that has dimensions in a Hilbert space of arity RANK, it may have some frequencies, and some parameters to communicate towards the user.
Inherited DimensionsBookkeeper::Dimensions
Pure virtual.
Pure virtual.
In the language of the framework, a free system is a system whit arity 1.
Inherits publicly from QuantumSystem<1> and DynamicsBase
Simply connects the pure virtual QuantumSystem::highestFrequency() to the implementation DynamicsBase::highestFrequency():
double highestFrequency () const {return DynamicsBase::highestFrequency();}
The same:
void displayParameters(std::ostream& os) const {return DynamicsBase::displayParameters(os);}
namespace free
This namespace contains some type definitions for convenience in defining free systems:
typedef for quantumoperator::Tridiagonal<1>:
typedef quantumoperator::Tridiagonal<1> Tridiagonal;
typedef for quantumoperator::Frequencies<1>:
typedef quantumoperator::Frequencies<1> Frequencies;
typedef quantumdata::Types<1>::StateVectorLow StateVectorLow;
typedef quantumdata::Types<1>::DensityOperatorLow DensityOperatorLow;
typedef quantumdata::LazyDensityOperator<1> LazyDensityOperator;
typedef quantumdata::StateVector<1> StateVector;
typedef quantumdata::DensityOperator<1> DensityOperator;
This class describes interaction between free systems.
template <int RANK> (cf. template parameters); inherits publicly from DynamicsBase
It does not inherit from QuantumSystem because it does not make sense to simulate such an element as describes an interaction alone. However, an interaction can have frequency-like parameters, hence the inheritance from DynamicsBase.
typedef blitz::TinyVector<const Free*,RANK> Frees;
The class has knowledge of its Free constituents, and will also communicate them.
An enumeration of the following possibilities for time dependence:
enum TimeDependence {TWO_TIME, ONE_TIME, NO_TIME};
| Case | TimeDependence | The Hamiltonian | |
|---|---|---|---|
| 1 | TWO_TIME |  |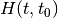
Time-dependent problem + exact part ( ) |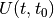
| 2 | ONE_TIME |  |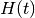
Time-dependent problem, no exact part |
| 3 | “ |  |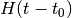
Time-independent problem + exact part ( ) |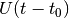
| 4 | NO_TIME |  |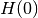
Time-independent problem, no exact part |
Where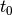 
is the time instant where the two pictures coincide.
template <int RANK, TimeDependence TD> (cf. template parameters);
Pure virtual.
Adds the Hamiltonian contribution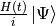 
of the given (sub)system to dpsidt assuming that the time when the Schrödinger picture and interaction picture (if any) coincide is tIntPic0. There are two important points to note:
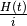and not merely 
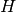, since it is the former which determines the derivative of the state vector. This is so often missed, that we emphasize it again (although we know that it will still be missed from time to time):Warning
When implementing the Hamiltonian, not
has to supplied!
For the class, we use partial specializations in the template parameter TimeDependent, and both cases ONE_TIME and NO_TIME inherit from TWO_TIME.
defines
virtual void addContribution(double, const StateVectorLow&, StateVectorLow&) const = 0;
and implements the above function as
void addContribution(double t, const StateVectorLow& psi, StateVectorLow& dpsidt, double tIntPic0) const
{
addContribution(t-tIntPic0,psi,dpsidt);
}
defines
virtual void addContribution(const StateVectorLow&, StateVectorLow&) const = 0;
and implements the above function as
void addContribution(double, const StateVectorLow& psi, StateVectorLow& dpsidt, double) const
{
addContribution(psi,dpsidt);
}
template <int RANK, bool IS_TD> (cf. template parameters); inherits publicly from Hamiltonian<RANK,ONE_TIME> when IS_TD=true and Hamiltonian<RANK,NO_TIME> when IS_TD=false. The present architecture of the classes Tridiagonal and Frequencies does not allow to cover the case TWO_TIME.
It implements the action of a Hamiltonian
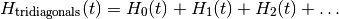
With the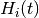 
being all described by Tridiagonal<RANK> objects, their time-dependence being described by corresponding Frequencies<RANK> objects.
Such a class can be constructed with either a list of Tridiagonal<RANK> (and, in the case when IS_TD is true, corresponding Frequencies<RANK>) objects, or only one such object when the above sum consists of only one term.
Experience shows that even when a system uses interaction picture (which is automatically the case if any of its subsystems does)—that is, part of its dynamics is solved exactly—it may still want to calculate the jump operators and quantum averages in the normal picture. (Cases 1 & 3 above.) This is useful e.g. to reuse the code written for the non-interaction-picture case.
In this case, the framework has to be provided with some means to transform between the two pictures. This is fulfilled by the following class, from which classes describing such systems have to inherit.
E.g. if MCWF_Trajectory sees that the simulated system inherits from Exact, then it will make the coherent part of the evolution in interaction picture, and then transform back to normal picture, so that all the rest (jump probabilities, eventual jumps, calculation of quantum averages) can take place in this latter picture. This makes that the two pictures coincide before each timestep. (Cf. also the stages described in Sec. MCWF trajectory.)
template <int RANK> (cf. template parameters).
Pure virtual.
Describes the operation which transforms from interaction picture to the normal picture.
Pure virtual.
Describes whether the above operation is unitary.
template <int RANK, bool IS_TD> (cf. template parameters), we use partial specialization in the second parameter, as with Hamiltonian:
This is just a TTD_DArray<1>.
Pure virtual. The first argument is missing when IS_TD=false.
It is always possible to forgo the explicit calculation of certain probabilities because the probability can be calculated also on the basis of the actWithJ() by the MCWF stepper. The fact that such a fallback is desired can be signalled by setting a negative value for the probability of the given jump (“special jump”).
Pure virtual. The first argument is missing when IS_TD=false. The last argument describes which jump is to be performed (a system may define several, assigning an ordinal to each of them).
template <int RANK, bool IS_TD> (cf. template parameters), the same holds for the time-dependence as with Liouvillean.
This is just a TTD_DArray<1>.
template<typename T> (T should model both Hamiltonian and DimensionsBookkeeper)
Calculates the matrix of a Hamiltonian of arbitrary rank.
Note
This works correctly only in Schrödinger picture!
Footnotes
| [1] | Note that this figure is tentative, and does not fully reflect the actual situation, which cannot be displayed in such a way either, due to the heavy use of templates, partial specializations, and conditional inheritance. |