The `quantumoperator` namespace¶

Representing “tridiagonal” matrices¶

Synopsis¶

Let us consider the following situation, which displays the full potential of the Tridiagonal class: We have a system consisting of 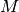$M$ subsystems, each featuring a free (in general, non-Hermitian) Hamiltonian, which is diagonal in the given system’s Hilbert space. In addition, we have one more term of a special form in the Hamiltonian coupling all the subsystems (we are considering 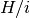$H/i$ , because this is what appears in the framework as noted here):

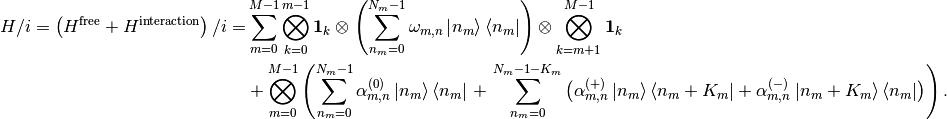
(1) $H/i=\lp H^\text{free}+H^\text{interaction}\rp/i=&\sum_{m=0}^{M-1}\bigotimes_{k=0}^{m-1}\mathbf{1}_k\otimes\lp\sum_{n_m=0}^{N_m-1}\omega_{m,n}\ket{n_m}\bra{n_m}\rp\otimes\bigotimes_{k=m+1}^{M-1}\mathbf{1}_k\\&+\bigotimes_{m=0}^{M-1}\lp\sum_{n_m=0}^{N_m-1}\alpha^{(0)}_{m,n}\ket{n_m}\bra{n_m}\right.+\left.\sum_{n_m=0}^{N_m-1-K_m}\lp\alpha^{(+)}_{m,n}\ket{n_m}\bra{n_m+K_m}+\alpha^{(-)}_{m,n}\ket{n_m+K_m}\bra{n_m}\rp\rp.$

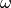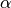Here, the coefficients $\omega$ and $\alpha$ are in general complex with the dimension of frequency ( 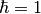$\hbar=1$ ). The 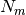$N_m$ s are the dimensions of the subsystems’ Hilbert spaces in which the vectors 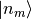$\ket{n_m}$ form an orthonormal basis.

The Hamiltonian is indeed in a special form because the interaction term is a direct product of such operators acting on the Hilbert spaces of the individual subsystems, whose matrix contains only three diagonals of nonzero elements. Hence the name of the class Tridiagonal, although this usually refers to the case when 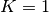$K=1$ .

Now let us transform to the interaction picture defined by 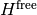$H^\text{free}$ . The Hamiltonian in interaction picture reads

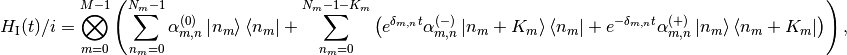
(2) $H\Int(t)/i=\bigotimes_{m=0}^{M-1}\lp\sum_{n_m=0}^{N_m-1}\alpha^{(0)}_{m,n}\ket{n_m}\bra{n_m}+\sum_{n_m=0}^{N_m-1-K_m}\lp e^{\delta_{m,n}t}\alpha^{(-)}_{m,n}\ket{n_m+K_m}\bra{n_m}+e^{-\delta_{m,n}t}\alpha^{(+)}_{m,n}\ket{n_m}\bra{n_m+K_m}\rp\rp,$

where 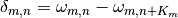$\delta_{m,n}=\omega_{m,n}-\omega_{m,n+K_m}$ .

Quite generally, the Tridiagonal class is designed to store and manipulate Hamiltonians of the form either (1) or (2) for an arbitrary number of subsystems. In the latter case, it also stores and manipulates the 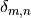$\delta_{m,n}$ frequencies. In particular, the Hamiltonian can be evaluated at a given time 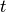$t$ , applied on a state vector and combined with other Tridiagonals using algebraic operations.

Tridiagonal internally bookkeeps to which time instant its state corresponds.

Policy of storing diagonals: only the non-zeros. Policy of storing frequencies: either none or all of them.

Tridiagonal can represent a diagonal matrix without significant overhead.

Note

The frequencies 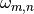$\omega_{m,n}$ are not necessarily real here, Tridiagonal works also for non-Hermitian operators. On non-unitary transformations in quantum mechanics these notes.

Implementation¶

Template argument definitions

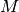int RANK: Positive integer standing for the number $M$ of elementary Hilbert spaces in (2)

class quantumoperator::Tridiagonal¶

template <int RANK> (cf. template parameters); inherits publicly from DimensionsBookkeeper<RANK,false>, and privately from linalg::VectorSpace<Tridiagonal<RANK> > which adds a lot of free-standing arithmetic functions

Types

LENGTH¶

The number of Diagonals the class has to store:

static const int LENGTH=tmptools::Power<3,RANK>::value;

N_RANK¶: Reports the class’s rank for example towards DirectProduct.

type Diagonals¶

The class is implemented in terms of a blitzplusplus::TinyOfArrays, this is the class used to store the Diagonals:

typedef blitzplusplus::TinyOfArrays<dcomp,RANK,LENGTH> Diagonals;

type Diagonal¶

typedef typename Diagonals::T_numtype Diagonal;

type Dimensions¶: Inherited from DimensionsBookkeeper

type StateVectorLow¶

typedef typename quantumdata::Types<RANK>::StateVectorLow StateVectorLow;

type IntRANK¶

(private) used for terser member-function signatures

typedef mpl::int_<RANK> IntRANK;

_1_¶

(private) used for terser member-function signatures

static const mpl::int_<1> _1_;//=mpl::int_<1>();

empty¶

(private) used for terser member-function signatures

static const Diagonal empty;//=Diagonal();

Constructors, assignment

explicit Tridiagonal(const Diagonal& zero=empty, size_t k=0, const Diagonal& minus=empty, const Diagonal& plus=empty, bool toFreqs=false, IntRANK one=_1_)¶

This is the principal way to create an object of this class, which can be used in the unary case only, as ensured by the trailing dummy argument. This creates an object corresponding to the elementary operator

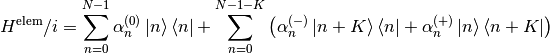
(3) $H^\text{elem}/i=\sum_{n=0}^{N-1}\alpha^{(0)}_n\ket{n}\bra{n}+\sum_{n=0}^{N-1-K}\lp\alpha^{(-)}_n\ket{n+K}\bra{n}+\alpha^{(+)}_n\ket{n}\bra{n+K}\rp$

when toFreq=false and

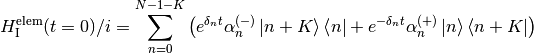
(4) $H\Int^\text{elem}(t=0)/i=\sum_{n=0}^{N-1-K}\lp e^{\delta_{n}t}\alpha^{(-)}_n\ket{n+K}\bra{n}+e^{-\delta_{n}t}\alpha^{(+)}_n\ket{n}\bra{n+K}\rp$

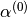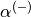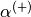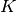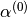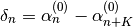when toFreq=true. The arguments zero, minus, plus, and k correspond respectively to $\alpha^{(0)}$ , $\alpha^{(-)}$ , $\alpha^{(+)}$ , and $K$ . In case of toFreq=true, the $\delta$ frequencies are calculated out of $\alpha^{(0)}$ as $\delta_{n}=\alpha^{(0)}_{n}-\alpha^{(0)}_{n+K}$ .

Either of the three initializing arrays might be zero-size, which signifies that the corresponding diagonal is zero, however, if they are nonzero-size, then their sizes must be compatible with each other. If both minus and plus are zero-size (purely diagonal matrix), then k might be zero as well. Violation is detected at runtime, and an exception of type TridiagonalConsistencyErrorException is thrown.

Note

It is a dilemma whether the parameter k should be considered a compile-time or a runtime parameter. In the majority of cases it is known already an compile time (e.g. ladder operators, angular momentum operators, etc.). The reason why it is treated as a runtime parameter is spatial degrees of freedom. There, operators like 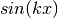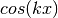$sin(kx)$ , $cos(kx)$ , etc., are also tridiagonal in momentum space, and we wanted to have to possibility of specifying 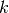$k$ at runtime.

Tridiagonal(const Tridiagonal& tridiag)¶: Copy constructor with deep-copy semantics.

Tridiagonal(const Tridiagonal<RANK2>& tridiag1, const Tridiagonal<RANK-RANK2>& tridiag2)¶

template <int RANK2>

Constructing the object as the direct product of tridiag1 and tridiag2. This is rather non-trivial, and the calculation of the resulting diagonals’ position is at the moment calculated at runtime, though it could partly be done at compile time. The eventual frequencies are also composed, direct product translates to a “direct sum” in this case. This really makes sense only if the time instants of the two tridiagonals are the same. Violation is detected at runtime, and an exception of type TridiagonalTimeMismatchException is thrown.

All tridiagonals of RANK>1 originate from direct products of unary tridiagonals.

Tridiagonal& furnishWithFreqs(const Diagonal& mainDiagonal, IntRANK one=_1_)¶: Furnishes a unary tridiagonal with frequencies calculated from mainDiagonal. Note that the matrix may have its own main diagonal in this case, which remains untouched. (This is actually exploited if we want to transform out only part of a main diagonal with interaction picture.) Returns *this.

Algebra

Note

At the moment, tridiagonal algebra is meant to be performed in the startup phase of simulations only, therefore, here we do not strive too much to optimize efficiency.

const Tridiagonal hermitianConjugate() const¶

const Tridiagonal dagger() const¶

Returns a newly constructed object, which is the Hermitian conjugate of this. Transposition involves a non-trivial permutation of diagonals, which could be done at compile-time, but at the moment it’s runtime.

Frequencies need not be transposed, because they are identical to their transpose.

Note

Eventually, an in-place version of Hermitian conjugation could be also implemented, if need for this arises.

Tridiagonal& operator+=(const Tridiagonal& tridiag)¶: Naive addition. The structures of the two objects must match, and there is a rather complicated set of rules as to what is meant by “matching”. Tridiagonal freely mixes with a purely diagonal matrix throught addition. If both have off-diagonals as well, the ks must match. If both store frequencies, they must be equal. Any violation of these rules is detected at runtime, and an exception of type TridiagonalStructureMismatchException is thrown.

const Tridiagonal operator-() const¶: Returns a (deep) copy with negated diagonals. Frequencies remain untouched.

const Tridiagonal operator+() const¶: Returns a (deep) copy.

Tridiagonal& operator-=(const Tridiagonal& tridiag)¶

Tridiagonal& operator-=(const Tridiagonal& tridiag) {(*this)+=-tridiag; return *this;}

Tridiagonal& operator*=(const dcomp& dc)¶

Tridiagonal& operator/=(const dcomp& dc)¶

Tridiagonal& operator*=(double d)¶

Tridiagonal& operator/=(double d)¶: Naively implemented, could be templated if need arises. Frequencies untouched throughout.

Class-specific functionality

Tridiagonal& propagate(double t)¶: Updates the elements of the matrix to time instant t with the help of the stored frequencies.

void apply(const StateVectorLow& psi, StateVectorLow& psiprime) const¶

“Applies” the tridiagonal matrix on the state vector psiprime, in the vein of structure::Hamiltonian::addContribution(), that is 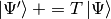$\ket{\Psi'}+=T\ket\Psi$ .

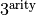Finding out which of the $3^{\text{arity}}$ diagonals corresponds to which state-vector slice when “applying”, is a formidable task for higher arity, and a significant portion of this calculation is done at compile time. The structure of this problem naturally maps to a recursion. There are 2 possibilities:

Explicit specializations of the function apply(). In this case, explicitly specialized code must be generated with the Python script quantumoperator/applyImpl/generate.py for each RANK (the Python script takes the rank as its first parameter in the command line). The user is encouraged to try it out to see the structure of the problem.

Here, the recursion inherent in the problem is shifted to this Python script. This solution sidesteps template metaprogramming, however, it has the drawback that the amount of code such produced grows exponentially with the arity.

This possibility is used if the DO_CONSIDER_EXPLICITLY_SPECIALIZED_TRIDIAGONAL_APPLIES macro is defined at compilation.
The function is implemented using the recursive doApply(), whose second version is present to break the recursivity. In this case, only this second version of the doApply() function must be explicitly specialized, which results in much less code.

This possibility is used if the DO_CONSIDER_EXPLICITLY_SPECIALIZED_TRIDIAGONAL_APPLIES macro is not defined at compilation.

Note

(Perhaps somewhat surprisingly,) compile-time resource requirement is larger in the 1st case.

The following four entities are private, serving as helpers for apply() in the 2nd case:

void doApply(mpl::int_<REMAINING> dummy, const Ranges& ranges, const StateVectorLow& psi, StateVectorLow& psiprime) const¶: template<int START, typename V_DPSIDT, typename V_A, typename V_PSI, int REMAINING>

void doApply(mpl::int_<0> dummy, const Ranges& ranges, const StateVectorLow& psi, StateVectorLow& psiprime) const¶

template<int START, typename V_DPSIDT, typename V_A, typename V_PSI>

This is explicitly specialized for all RANKs, with the help of preprocessor metaprogramming. We rely on the Boost.Preprocessor library, in particular the BOOST_PP_ITERATE macro. The reentrant header can be found at quantumoperator/details/TridiagonalApplySpecialization.h.

class FillRangesHelper¶

const Ranges fillRanges(const StateVectorLowIndexType& idx) const¶

Free-standing helpers

const Tridiagonal<1> zero(size_t dim)¶

const Tridiagonal<1> identity(size_t dim)¶

const Tridiagonal<RANK> quantumoperator::furnishWithFreqs(const Tridiagonal<RANK>& tridiag, const Diagonal& mainDiagonal)¶: At the moment only for the unary case, implemented in terms of quantumoperator::Tridiagonal::furnishWithFreqs().

Note

A serious limitation of Tridiagonal is that the composition of two such operators does not in general yield an operator of the same form. This is one of the reasons why we are planning to deprecate Tridiagonal in favour of a much more general form

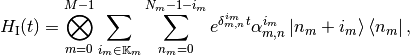
$H\Int(t)=\bigotimes_{m=0}^{M-1}\sum_{i_m\in\mathbb{K}_m}\sum_{n_m=0}^{N_m-1-i_m}e^{\delta^{i_m}_{m,n}t}\alpha^{i_m}_{m,n}\ket{n_m+i_m}\bra{n_m},$

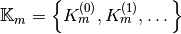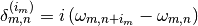with $\mathbb{K}_m=\left\{K_m^{(0)},K_m^{(1)},\dots\right\}$ an arbitrary set, and $\delta_{m,n}^{(i_m)}=i\lp\omega_{m,n+i_m}-\omega_{m,n}\rp$ .

Sigma¶

class quantumoperator::Sigma¶

template<int L, int R>

Stateless class implementing the unary quantumoperator

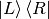
$\ket{L}\bra{R}$

The template parameters are eventually converted to runtime data when applying the operator. At that point, dimensionality errors are detected in debug mode. All members are fairly trivial:

N_RANK

static const int N_RANK=1;

type StateVectorLow¶

typedef quantumdata::Types<1>::StateVectorLow

void apply(const StateVectorLow& psi, StateVectorLow& dpsidt) const¶

{dpsidt(L)+=psi(R);}

const Sigma<R, L> dagger() const¶

{return Sigma<R,L>();}

Note

Sigma should perhaps inherit from DimensionsBookkeeper—this would allow for an earlier detection of dimensionality errors.

class quantumoperator::DirectProduct¶

template<int L, int R, typename OTHER, bool IS_HEAD>

This class is a direct-product clause, representing a germinal expression-template mechanism for direct products of Sigma<L,R> with OTHER types.

Models for OTHER at the moment:

Another class Sigma<L1,R1>
A Tridiagonal type
Another DirectProduct (recursivity)

IS_HEAD signifies whether Sigma<L,R> is at the head or at the tail of the direct product.

N_RANK

Reports the rank of the class for recursive usage:

static const int N_RANK=OTHER::N_RANK+1;

type StateVectorLow¶

typedef typename quantumdata::Types<N_RANK>::StateVectorLow StateVectorLow;

DirectProduct(const OTHER& other)¶: The class has to store a reference to the OTHER class to enable apply()ing.

void apply(const StateVectorLow& psi, StateVectorLow& dpsidt) const¶: Applies the clause on a state vector psi, adding the result to dpsidt, analogously to quantumoperator::Tridiagonal::apply() and structure::Hamiltonian::addContribution(). It is implemented as taking the partial projection of the state vectors according to L and R (which at this point are converted into runtime data), and calling the apply function of the OTHER type.

Free-standing helpers

const DirectProduct<L, R, OTHER, true> quantumoperator::operator*(const Sigma<L, R>& head, const OTHER& tail)¶: template<int L, int R, typename OTHER>

const DirectProduct<L, R, OTHER, false> quantumoperator::operator*(const OTHER& head, const Sigma<L, R>& tail)¶: template<int L, int R, typename OTHER>

const DirectProduct<L1, R1, Sigma<L2, R2>, true> quantumoperator::operator*(const Sigma<L1, R1>& head, const Sigma<L2, R2>& tail)¶

template<int L1, int R1, int L2, int R2>

These operators aptly demonstrate the use of DirectProduct and the meaning of its template parameters:

const StateVectorLow<RANK-1> quantumoperator::partialProject(const StateVectorLow<RANK>& psi, int n)¶

template<int RANK, bool IS_HEAD>

Helper for quantumoperator::DirectProduct::apply(). Calculates the state-vector slice

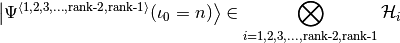
$\ket{\Psi^{\avr{1,2,3,…,\text{rank-2},\text{rank-1}}}(\iota_0=n)}\in\bigotimes_{i=1,2,3,…,\text{rank-2},\text{rank-1}}\HSpace_i$

if IS_HEAD=true and

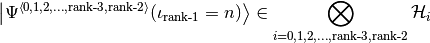
$\ket{\Psi^{\avr{0,1,2,…,\text{rank-3},\text{rank-2}}}(\iota_\text{rank-1}=n)}\in\bigotimes_{i=0,1,2,…,\text{rank-3},\text{rank-2}}\HSpace_i$

if IS_HEAD=false.

The code is automatically generated for all template-parameter combinations (RANK up to 11) via preprocessor metaprogramming. Cf. quantumoperator::Sigma.cc:

g++ -P -E -Iutils/include/ -Iquantumoperator/ -Iquantumdata/ quantumoperator/Sigma.cc | tail -n128

Table Of Contents

Previous topic

Next topic

The `quantumoperator` namespace¶

Representing “tridiagonal” matrices¶

Synopsis¶

Implementation¶

Sigma¶

Navigation

Table Of Contents

Previous topic

Next topic

Quick search

The quantumoperator namespace¶

Representing “tridiagonal” matrices¶

Synopsis¶

Implementation¶

Sigma¶

Navigation

The `quantumoperator` namespace¶