C++QEDCore  v2 Milestone 10
a framework for simulating open quantum dynamics – core
Classes | Public Types | Public Member Functions | Protected Member Functions | Friends | List of all members
quantumdata::LazyDensityOperator< RANK > Class Template Referenceabstract

Common interface for calculating quantum averages. More...

#include <LazyDensityOperator.h>

+ Inheritance diagram for quantumdata::LazyDensityOperator< RANK >:
+ Collaboration diagram for quantumdata::LazyDensityOperator< RANK >:

Public Types

typedef boost::shared_ptr< const LazyDensityOperator > Ptr
 Many class templates in the framework define shared pointers to their own types, in a template-metafunction like manner.
 
typedef DimensionsBookkeeper< RANK, true > Base
 
typedef Base::Dimensions Dimensions
 Inherited from DimensionsBookkeeper.
 
typedef IdxTiny< RANK > Idx
 The type used for indexing the “rows” and the “columns”: a tiny vector of integers (multi-index)
 
- Public Types inherited from DimensionsBookkeeper< RANK, true >
typedef ExtTiny< RANK > Dimensions
 The dimensions as a static vector of size N_RANK.
 

Public Member Functions

const IndexerProxy operator() (const Idx &firstIndex) const
 Multi-matrix style indexing via Idx type.
 
template<typename... SubscriptPack>
const IndexerProxy operator() (int s0, SubscriptPack...subscriptPack) const
 Multi-matrix style indexing via packs of integers. More...
 
double trace () const
 Returns the trace (redirected to a pure virtual)
 
Slicing-related functionality
template<typename V >
const ldo::DiagonalIterator< RANK, V > begin () const
 Return the ldo::DiagonalIterator corresponding to the beginning of the sequence of slices defined by V More...
 
template<typename V >
const ldo::DiagonalIterator< RANK, V > end () const
 ” for the end
 
- Public Member Functions inherited from DimensionsBookkeeper< RANK, true >
 DimensionsBookkeeper (mpl::bool_< IS_CONST >=mpl::false_())
 Constructor usable only in the IS_CONST=false case. More...
 
 DimensionsBookkeeper (const Dimensions &dimensions)
 Standard constructor usable also in the IS_CONST=true case.
 
const Dimensions & getDimensions () const
 Get the Dimensions vector.
 
size_t getTotalDimension () const
 Get the total dimension of a system of arbitrary arity.
 
size_t getDimension (mpl::int_< RANK >=mpl::int_< 1 >()) const
 Get the (single) dimension for a unary system.
 
size_t getDimension (size_t i) const
 
void setDimensions (const Dimensions &dimensions)
 This will work only in the non-const case.
 

Protected Member Functions

 LazyDensityOperator (const Dimensions &dims)
 

Friends

class IndexerProxy
 

Additional Inherited Members

- Static Public Attributes inherited from DimensionsBookkeeper< RANK, true >
static const int N_RANK
 Arity of the Hilbert space.
 
static const int DIMESIONS_BOOKKEEPER_RANK
 Ditto (to break ambiguity if a class is derived from another base featuring N_RANK).
 

Detailed Description

template<int RANK>
class quantumdata::LazyDensityOperator< RANK >

Common interface for calculating quantum averages.

In a quantum-simulation framework, users should be able to write code for calculating quantum expectation values from quantumdata, independently of whether this data is represented by state vectors or density operators, in orthogonal or non-orthogonal bases. One obvious solution is relying on the formula

\[\avr{A}=\Tr{A\rho}\]

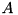( $A$ being an observable and 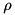$\rho$ the density operator of the system), to write code only for the density-operator case, and fall back to this in the state-vector case as well, by calculating a dyad from the state vector. 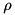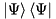This is, however, extremely wasteful, since usually not all the matrix elements of $\rho$ are needed for calculating the average, furthermore, for large dimensionality, this solution may become outright unaffordable in terms of memory: for large systems, we may afford to store $\ket\Psi$, but not $\ket\Psi\bra\Psi$.

The solution adopted for this problem in the framework is represented by LazyDensityOperator, which provides a common interface for all the four cases StateVector, DensityOperator, and their non-orthogonal counterparts, to calculate quantum averages from their data. The “laziness” amounts to that in the case of state vectors, only those elements of the density operator are calculated that are actually asked for.

This class is totally immutable, all its member functions being constant.

Template Parameters
RANKarity of the Hilbert space
Semantics
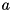  • Unary system: Assume a mode represented in Fock basis with ladder-operator $a$. To calculate the quantum expectation value

    \[\avr{a^2}=\Tr{a^2\rho}=\sum_i\sqrt{i(i-1)}\,\rho_{i;i-2},\]

    one can write the following function:

~~~ include "LazyDensityOperator.h"

const dcomp calculateASqr(const LazyDensityOperator<1>& matrix) { dcomp res; for (int i=2; i<matrix.getTotalDimension(); ++i) res+=sqrt(i*(i-1))*matrix(i,i-2); return res; }

  • ~~~
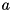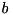    • Binary system: Assume two modes represented in Fock bases with ladder-operators $a$ and $b$, respectively. To calculate the quantum expectation value

      \[\avr{a^\dag b}=\Tr{a^\dag b\rho}=\sum_{i,j}\sqrt{(i+1)j}\,\rho_{(i,j);(i+1,j-1)},\]

      one can write the following function:

  • ~~~ include "LazyDensityOperator.h"

    const dcomp calculateADaggerB(const LazyDensityOperator<2>& matrix) { const LazyDensityOperator<2>::Dimensions dim(matrix.getDimensions());

    dcomp res; for (int i=0; i<dim[0]-1; ++i) for (int j=1; j<dim[1]; ++j) res+=sqrt((i+1)*j)*matrix(i,j)(i+1,j-1); return res; }

  • ~~~

Definition at line 61 of file LazyDensityOperator.h.

Member Function Documentation

template<int RANK>
template<typename V >
const ldo::DiagonalIterator<RANK,V> quantumdata::LazyDensityOperator< RANK >::begin ( ) const

Return the ldo::DiagonalIterator corresponding to the beginning of the sequence of slices defined by V

Cf. rationale

Template Parameters
Vcompile-time vector holding the retained index positions (cf. Specifying subsystems)
template<int RANK>
template<typename... SubscriptPack>
const IndexerProxy quantumdata::LazyDensityOperator< RANK >::operator() ( int  s0,
SubscriptPack...  subscriptPack 
) const
inline

Multi-matrix style indexing via packs of integers.

This allows for the very convenient indexing syntax (e.g. a ternary LazyDensityOperator matrix indexed by multi-indeces i and j): 

matrix(i0,i1,i2)(j0,j1,j2)

while 

matrix(i0,i1,i2)

returns a proxy implicitly convertible to a double, giving the diagonal element corresponding to the multi-index i

Note
The number of indeces in the multi-index is checked @ compile time.

Definition at line 120 of file LazyDensityOperator.h.

The documentation for this class was generated from the following file: