Comprises classes representing the state of composite quantum systems and providing various interfaces to manipulate this data. More...

Namespaces
	ldo
	Comprises tools related to LazyDensityOperator, like DiagonalIterator.

	transformation
	Comprises tools for metric transformations of NonOrthogonalStateVector and NonOrthogonalDensityOperator classes.

Classes
class	ArrayBase
	Comprises the common functionalities of StateVector and DensityOperator. More...

class	DensityOperator
	Density operator of arbitrary arity. More...

class	LazyDensityOperator
	Common interface for calculating quantum averages. More...

struct	LazyDensityOperatorFFT_NotImplementedException

class	NonOrthogonalStateVector

struct	ParsFunctionScan
	Parameter set for scanFunction. More...

class	StateVector
	State vector of arbitrary arity. More...

struct	TensorType

struct	Types
	Basically only a metafunction defining types for higher-level constructs of arity `RANK` More...

class	WignerFunctionKernelOld

Functions
template<int RANK>
const DensityOperator< RANK >	dyad (const StateVector< RANK > &, const StateVector< RANK > &)

template<int RANK1, int RANK2>
const DensityOperator< RANK1+RANK2 >	operator* (const DensityOperator< RANK1 > &, const DensityOperator< RANK2 > &)

template<int RANK>
double	frobeniusNorm (const DensityOperator< RANK > &rho)

template<int RANK>
void	inflate (const DArray< 1 > &, DensityOperator< RANK > &, bool offDiagonals)
	Performs the opposite of quantumdata::deflate.

template<int RANK>
const DensityOperator< RANK >	densityOperatorize (const LazyDensityOperator< RANK > &)
	Creates a DensityOperator as the (deep) copy of the data of a LazyDensityOperator of the same arity.

template<int... SUBSYSTEM, int RANK>
const DensityOperator< mpl::size< tmptools::Vector< SUBSYSTEM... > >::value >	reduce (const LazyDensityOperator< RANK > &)

template<typename DensityOperatorFunctor >
double	wignerFunction (const DensityOperatorFunctor &rho, double x, double y, size_t truncatedDimension=0)
	Calculates the Wigner function corresponding to a harmonic-oscillator mode density matrix expressed in Fock basis. More...

template<typename DensityOperator >
double	qFunction (const DensityOperator &rho, double x, double y, size_t)

template<typename DensityOperatorFunctor >
double	wignerFunctionOld (const DensityOperatorFunctor &rho, double x, double y, size_t truncatedDimension=0)

template<typename DistributionFunctor , typename DensityOperator >
std::ostream &	scanFunction (DistributionFunctor distributionFunctor, const DensityOperator &rho, std::ostream &os, const ParsFunctionScan &pfs)
	Creates a map of the Wigner function over the region specified by `pfs` and streams it in a format suitable for gnuplot pm3d maps.

template<typename V , typename T , int RANK, typename F >
const T	partialTrace (const LazyDensityOperator< RANK > &, F function)
	The primary tool for performing slice iterations. More...

template<int RANK>
const DArray< 1 >	deflate (const LazyDensityOperator< RANK > &, bool offDiagonals)
	Turns the data of a LazyDensityOperator into a real 1D array. More...

void	ffTransform (linalg::CVector &, fft::Direction)

void	ffTransform (linalg::CMatrix &, fft::Direction)

template<typename V , int RANK>
const boost::shared_ptr< const LazyDensityOperator< RANK > >	ffTransform (const LazyDensityOperator< RANK > &, fft::Direction)

template<int RANK, typename V >
double	negPT (const DensityOperator< RANK > &, V)
	Calculates the negativity of the partial transpose of the density operator of an arbitrarily complex system. More...

template<int RANK>
double	negPT (const DensityOperator< RANK > &, tmptools::V_Empty)

template<int RANK1, typename TRAFO1 , int RANK2, typename TRAFO2 >
const NonOrthogonalStateVector< RANK1+RANK2, typename transformation::Compose< TRAFO1, TRAFO2 >::type >	operator* (const NonOrthogonalStateVector< RANK1, TRAFO1 > &sv1, const NonOrthogonalStateVector< RANK2, TRAFO2 > &sv2)

template<int RANK1, typename TRAFO1 , int RANK2>
const NonOrthogonalStateVector< RANK1+RANK2, typename transformation::Compose< TRAFO1, transformation::Identity< RANK2 > >::type >	operator* (const NonOrthogonalStateVector< RANK1, TRAFO1 > &sv1, const StateVector< RANK2 > &sv2)

template<int RANK1, int RANK2, typename TRAFO2 >
const NonOrthogonalStateVector< RANK1+RANK2, typename transformation::Compose< transformation::Identity< RANK1 >, TRAFO2 >::type >	operator* (const StateVector< RANK1 > &sv1, const NonOrthogonalStateVector< RANK2, TRAFO2 > &sv2)

template<int RANK1, int RANK2>
const StateVector< RANK1+RANK2 >	operator* (const StateVector< RANK1 > &, const StateVector< RANK2 > &)
	Creates the direct product, relying on the direct-product constructor.

template<int RANK>
const dcomp	braket (const StateVector< RANK > &, const StateVector< RANK > &)
	Calculates the inner product, relying on StateVector::vectorView.

Detailed Description

Comprises classes representing the state of composite quantum systems and providing various interfaces to manipulate this data.

Some of its most important classes fit into a single class rooted in the virtual interface LazyDensityOperator.

Function Documentation

template<int RANK>

const DArray<1> quantumdata::deflate	(	const LazyDensityOperator< RANK > &	,
		bool	offDiagonals
	)

Turns the data of a LazyDensityOperator into a real 1D array.

The result is an array starting with the diagonals (real) of the matrix, optionally followed by the off-diagonals (real & imaginary) of the upper triangle. For this to make sense, the matrix is assumed to be Hermitian.

Parameters

offDiagonals governs whether the upper triangle of the (multi-)matrix is included in the result

template<int RANK, typename V >

double quantumdata::negPT	(	const DensityOperator< RANK > &	,
		V
	)

Calculates the negativity of the partial transpose of the density operator of an arbitrarily complex system.

See also: [9]

The system should of course be regarded as a bipartite system, so that a subsystem has to be specified to be one part of the bipartite. The compile-time vector V specifies the subsystem.

The negativity is calculated as the sum of the negative eigenvalues of the partially transposed density operator.

Note

This definition is equivalent to the original definition [9] up to a sign, because the partially transposed density operator's eigenvalues come in two sorts:

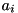solitary positive numbers ( ) adding up to one, and
pairs of opposite-sign numbers ( ).

Hence

$\mathcal{N}(\rho)\equiv\frac{\norm{\rho^{\text{PT}}}_1-1}2=\frac{\sum_i\abs{\rho^{\text{PT}}_{ii}}-1}2=\frac{\sum_ia_i+2\sum_ib_i-1}2=\sum_ib_i.$

Template Parameters

RANK	arity of the Hilbert space
V	a compile-time vector, tipically a tmptools::Vector, specifying the quantum numbers grouped into one part of the bipartite (cf. Specifying subsystems)

template<typename V , typename T , int RANK, typename F >

template< typename V, typename T, int RANK, typename F > const T quantumdata::partialTrace	(	const LazyDensityOperator< RANK > &	,
		F	function
	)

The primary tool for performing slice iterations.

On higher levels of the framework (cf. eg. BinarySystem, Composite), this function is used exclusively for performing LazyDensityOperator slice iteration.

Template Parameters

V	compile-time vector holding the retained index positions (cf. Specifying subsystems)
T	an arithmetic type which must be default-constructible
F	a callable type with signature `const T(const typename ldo::DiagonalIterator<RANK,V>::value_type&)`. This signature is equivalent to `const T(const LazyDensityOperator<mpl::size<V>::value>&)`.

Semantics

The function iterates through all the combinations of the dummy indices, for each slice it takes the value returned by the functor function, and accumulates these values. In the following we give some instructive examples of usage.

Calculating the full partial density operator of a unary subsystem: The partial density operator of any unary subsystem of a system of any rank may be calculated as follows (e.g. from a StateVector):

~~~ template<int SUBSYSTEM, int RANK> // for the subsystem indexed by the index SUBSYSTEM const DensityOperator<1> partialTraceOfUnarySubsystem(const StateVector<RANK>& psi) { return partialTrace<tmptools::Vector<SUBSYSTEM>,DensityOperator<1> >(psi,densityOperatorize<1>); }

~~~
- Calculating correlations for two harmonic-oscillator modes: Assume having the function calculateADaggerB as defined @ LazyDensityOperator. Then, if these modes are embedded at index positions 3 and 1 (note that the order might be important) in a larger system of arity larger than 3, we can write the following function: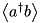
~~~ template<int RANK> // RANK>3 const dcomp calculateADaggerB_atPositions3and1(const LazyDensityOperator<RANK>& matrix) { return partialTrace<tmptools::Vector<3,1>,dcomp>(matrix,calculateADaggerB); }
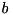~~~ This will calculate (now and 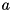being the ladder operators of the modes at position 1 and 3, respectively) for the partial density operator of the embedded system (but without explicitly calculating this partial density operator).
- Accumulating an arbitrary set of quantum averages: An arbitrary set of real or complex numbers can be stored in a DArray<1> or CArray<1> (or even std::valarrays), as these types fulfill all the requirements on type T. The former was used to define the abstract interface structure::Averaged one of its implementations being :class:Mode. E.g. a function for a harmonic-oscillator mode calculating 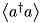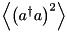$\avr{a^\dag a}$ , $\avr{\lp a^\dag a\rp^2}$ , and the real and imaginary parts of 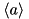$\avr{a}$ , may be defined as
~~~ typedef DArray<1> Averages;

const Averages calculateModeAverages(const LazyDensityOperator<1>& matrix) { Averages averages(4); averages=0;

for (int n=1; n<int(matrix.getDimension()); n++) { double diag=matrix(n); averages(0)+= n*diag; averages(1)+=n*n*diag;

double sqrtn=sqrt(n); dcomp offdiag(matrix(n,n-1)); averages(2)+=sqrtn*real(offdiag); averages(3)+=sqrtn*imag(offdiag); }

return averages;

}
~~~ Then the following function will calculate these averages for a mode embedded in a larger system at index position MODE_POSITION:
~~~ template<int RANK, int MODE_POSITION> // for the subsystem indexed by the index MODE_POSITION const Averages calculateEmbeddedModeAverages(const StateVector<RANK>& psi) { return partialTrace(psi,calculateModeAverages,tmptools::Vector<MODE_POSITION>(),Averages()); }
~~~

template<typename DensityOperatorFunctor >

double quantumdata::wignerFunction	(	const DensityOperatorFunctor &	rho,
		double	x,
		double	y,
		size_t	truncatedDimension = `0`
	)

Calculates the Wigner function corresponding to a harmonic-oscillator mode density matrix expressed in Fock basis.

We use the formula given by Leonhardt [5]

$W[\rho](x,y)=w(r,0)+2\sum_{k=1}^M \real{w(r,k)\,e^{-i\,k\varphi}},$

with

$w(r,k)\equiv\sum_{n=0}^{M-k}\left[\frac1\pi(-1)^n\sqrt{\frac{n!}{(n-k)!}}\,e^{-2\,r^2}\lp2\,r\rp^k L_n^k\lp4\,r^2\rp\right]\rho_{n+k,n}.$

The difference of $\sqrt{2}$ in front of $r$ comes from our different definition of the quadratures: $x=\frac{a+a^\dagger}2,\;y=\frac{a-a^\dagger}{2i}$ . The quadratures are recalculated into polar coordinates: $x=r\,\cos\lp\varphi\rp\;y=r\,\sin\lp\varphi\rp$ .

Note

The function is wasteful at the moment from several points of view:

we do not use the recurrence formula (5.114) of the Leonhardt book
gets recalculated for each pair of $x\;y$ leaving unexploited that it depends only on

Template Parameters

DensityOperatorFunctor a type modelling a unary density operator

Parameters

truncatedDimension if nonzero, this is used as the dimension instead of the actual dimension of rho

Todo:: Should refer rho only via some traits class to make the code really generic.

Definition at line 59 of file DistributionFunctions.h.

Namespaces

Classes

Functions

Detailed Description

Function Documentation