Class representing a (unary) tridiagonal matrix or direct product of such matrices. More...
#include <Tridiagonal.h>
 Inheritance diagram for quantumoperator::Tridiagonal< RANK >:
Inheritance diagram for quantumoperator::Tridiagonal< RANK >: Collaboration diagram for quantumoperator::Tridiagonal< RANK >:
Collaboration diagram for quantumoperator::Tridiagonal< RANK >:Public Types | |
| typedef blitzplusplus::TinyOfArrays< dcomp, RANK, LENGTH > | Diagonals |
| The class is implemented in terms of a blitzplusplus::TinyOfArrays, this is the class used to store the Diagonals. | |
| typedef Diagonals::T_numtype | Diagonal |
| A unary complex blitz array. | |
| typedef Base::Dimensions | Dimensions |
| Inherited from DimensionsBookkeeper. | |
| typedef quantumdata::Types< RANK >::StateVectorLow | StateVectorLow |
 Public Types inherited from DimensionsBookkeeper< RANK > Public Types inherited from DimensionsBookkeeper< RANK > | |
| typedef ExtTiny< RANK > | Dimensions |
| The dimensions as a static vector of size N_RANK. | |
Public Member Functions | |
Constructors, assignment | |
| Tridiagonal (const Diagonal &zero=empty, size_t k=0, const Diagonal &minus=empty, const Diagonal &plus=empty, bool toFreqs=false, IntRANK=_1_) | |
| Constructor for unary Tridiagonal. More... | |
| Tridiagonal (const Tridiagonal &tridiag) | |
| Copy constructor with deep-copy semantics. | |
| template<int RANK2> | |
| Tridiagonal (const Tridiagonal< RANK2 > &, const Tridiagonal< RANK-RANK2 > &) | |
| Constructs the object as the direct product of two Tridiagonal matrices. More... | |
Class-specific functionality | |
| Tridiagonal & | furnishWithFreqs (const Diagonal &mainDiagonal, IntRANK=_1_) |
Furnishes a unary tridiagonal with frequencies calculated from mainDiagonal. More... | |
| void | apply (const StateVectorLow &psi, StateVectorLow &dpsidt) const |
“Applies” the tridiagonal matrix on the state vector psiprime, in the vein of structure::Hamiltonian::addContribution(), that is 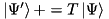 . More... . More... | |
| Tridiagonal & | propagate (double t) |
Updates the elements of the matrix to time instant t using the stored frequencies. More... | |
| const dcomp | average (const quantumdata::LazyDensityOperator< RANK > &, const typename quantumdata::LazyDensityOperator< RANK >::Idx &, IntRANK=_1_) |
| Calculates the quantum average of a Tridiagonal in a quantum state described by a (unary) quantumdata::LazyDensityOperator. More... | |
Getters | |
| const Diagonals & | get () const |
| returns the diagonals | |
| const Dimensions & | getDifferences () const |
| double | getTime () const |
| const Diagonals & | getFreqs () const |
Algebra | |
| Tridiagonal & | operator*= (const dcomp &dc) |
| Naively implemented, could be templated if need arises – Frequencies untouched. | |
| Tridiagonal & | operator/= (const dcomp &dc) |
| ” | |
| Tridiagonal & | operator*= (double d) |
| ” | |
| Tridiagonal & | operator/= (double d) |
| ” | |
| const Tridiagonal | hermitianConjugate () const |
Returns a newly constructed object, which is the Hermitian conjugate of this. More... | |
| const Tridiagonal | dagger () const |
| Same as hermitianConjugate. | |
| Tridiagonal & | operator+= (const Tridiagonal &) |
| Naive addition. More... | |
| const Tridiagonal | operator- () const |
| Returns a (deep) copy with negated diagonals. Frequencies remain untouched. | |
| const Tridiagonal | operator+ () const |
| Returns a (deep) copy. | |
| Tridiagonal & | operator-= (const Tridiagonal &tridiag) |
| Implemented in terms of operator+=. | |
 Public Member Functions inherited from DimensionsBookkeeper< RANK > Public Member Functions inherited from DimensionsBookkeeper< RANK > | |
| DimensionsBookkeeper (mpl::bool_< IS_CONST >=mpl::false_()) | |
Constructor usable only in the IS_CONST=false case. More... | |
| DimensionsBookkeeper (const Dimensions &dimensions) | |
Standard constructor usable also in the IS_CONST=true case. | |
| const Dimensions & | getDimensions () const |
| Get the Dimensions vector. | |
| size_t | getTotalDimension () const |
| Get the total dimension of a system of arbitrary arity. | |
| size_t | getDimension (mpl::int_< RANK >=mpl::int_< 1 >()) const |
| Get the (single) dimension for a unary system. | |
| size_t | getDimension (size_t i) const |
| void | setDimensions (const Dimensions &dimensions) |
| This will work only in the non-const case. | |
Static Public Attributes | |
| static const int | LENGTH =tmptools::Power<3,RANK>::value |
| The number of Diagonals the class has to store. | |
| static const int | N_RANK =RANK |
| Reports the class’s rank for example towards DirectProduct. | |
 Static Public Attributes inherited from DimensionsBookkeeper< RANK > Static Public Attributes inherited from DimensionsBookkeeper< RANK > | |
| static const int | N_RANK |
| Arity of the Hilbert space. | |
| static const int | DIMESIONS_BOOKKEEPER_RANK |
Ditto (to break ambiguity if a class is derived from another base featuring N_RANK). | |
Related Functions | |
(Note that these are not member functions.) | |
| template<int RANK> | |
| void | apply (const typename quantumdata::Types< RANK >::StateVectorLow &psi, typename quantumdata::Types< RANK >::StateVectorLow &dpsidt, const Tridiagonal< RANK > &) |
| A free-standing version of Tridiagonal::apply. More... | |
| template<int RANK> | |
| const Tridiagonal< RANK > | furnishWithFreqs (const Tridiagonal< RANK > &tridiag, const typename Tridiagonal< RANK >::Diagonal &mainDiagonal) |
| Same as Tridiagonal::furnishWithFreqs, but returns a copy of its first argument furnished with frequencies. More... | |
| const Tridiagonal< 1 > | zero (size_t) |
| Unary zero operator as a Tridiagonal. More... | |
| const Tridiagonal< 1 > | identity (size_t) |
| Unary identity operator as a Tridiagonal. More... | |
| template<int RANK1, int RANK2> | |
| const Tridiagonal< RANK1+RANK2 > | operator* (const Tridiagonal< RANK1 > &t1, const Tridiagonal< RANK2 > &t2) |
| Direct product. More... | |
| template<int RANK> | |
| const Tridiagonal< RANK > | tridiagMinusHC (const Tridiagonal< RANK > &tridiag) |
Returns the anti-Hermitian operator  . More... . More... | |
| template<int RANK> | |
| const Tridiagonal< RANK > | tridiagPlusHC (const Tridiagonal< RANK > &tridiag) |
Returns the Hermitian operator 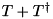 . More... . More... | |
| template<int RANK> | |
| const Tridiagonal< RANK > | tridiagPlusHC_overI (const Tridiagonal< RANK > &tridiag) |
Returns the anti-Hermitian operator 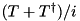 . More... . More... | |
| template<int RANK> | |
| std::ostream & | operator<< (std::ostream &, const Tridiagonal< RANK > &) |
Class representing a (unary) tridiagonal matrix or direct product of such matrices.
Let us consider the following situation, which displays the full potential of the class: We have a system consisting of 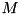 subsystems, each featuring a free (in general, non-Hermitian) Hamiltonian, which is diagonal in the given system’s Hilbert space. In addition, we have one more term of a special form in the Hamiltonian coupling all the subsystems (we are considering
subsystems, each featuring a free (in general, non-Hermitian) Hamiltonian, which is diagonal in the given system’s Hilbert space. In addition, we have one more term of a special form in the Hamiltonian coupling all the subsystems (we are considering  , because this is what appears in the framework as noted @ structure::Hamiltonian::addContribution):
, because this is what appears in the framework as noted @ structure::Hamiltonian::addContribution):
![\[H/i=\lp H^\text{free}+H^\text{interaction}\rp/i=\sum_{m=0}^{M-1}\bigotimes_{k=0}^{m-1}\mathbf{1}_k\otimes\lp\sum_{n_m=0}^{N_m-1}\omega_{m,n}\ket{n_m}\bra{n_m}\rp\otimes\bigotimes_{k=m+1}^{M-1}\mathbf{1}_k+\bigotimes_{m=0}^{M-1}\lp\sum_{n_m=0}^{N_m-1}\alpha^{(0)}_{m,n}\ket{n_m}\bra{n_m}\right.+\left.\sum_{n_m=0}^{N_m-1-K_m}\lp\alpha^{(+)}_{m,n}\ket{n_m}\bra{n_m+K_m}+\alpha^{(-)}_{m,n}\ket{n_m+K_m}\bra{n_m}\rp\rp.\]](form_150.png)
Here, the coefficients 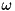 and
and  are in general complex with the dimension of frequency (
are in general complex with the dimension of frequency ( 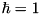 ). The
). The 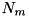 s are the dimensions of the subsystems’ Hilbert spaces in which the vectors
s are the dimensions of the subsystems’ Hilbert spaces in which the vectors 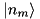 form an orthonormal basis.
form an orthonormal basis.
The Hamiltonian is indeed in a special form because the interaction term is a direct product of such operators acting on the Hilbert spaces of the individual subsystems, whose matrix contains only three diagonals of nonzero elements. Hence the name of the class Tridiagonal, although this usually refers to the case when 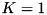 .
.
Now let us transform to the interaction picture defined by 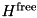 . The Hamiltonian in interaction picture reads
. The Hamiltonian in interaction picture reads
![\[H\Int(t)/i=\bigotimes_{m=0}^{M-1}\lp\sum_{n_m=0}^{N_m-1}\alpha^{(0)}_{m,n}\ket{n_m}\bra{n_m}+\sum_{n_m=0}^{N_m-1-K_m}\lp e^{\delta_{m,n}t}\alpha^{(-)}_{m,n}\ket{n_m+K_m}\bra{n_m}+e^{-\delta_{m,n}t}\alpha^{(+)}_{m,n}\ket{n_m}\bra{n_m+K_m}\rp\rp,\]](form_157.png)
where 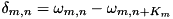 .
.
Quite generally, the class is designed to store and manipulate Hamiltonians of the form either  or
or 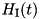 above for an arbitrary number of subsystems. In the latter case, it also stores and manipulates the
above for an arbitrary number of subsystems. In the latter case, it also stores and manipulates the 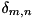 frequencies. In particular, the Hamiltonian can be evaluated at a given time
frequencies. In particular, the Hamiltonian can be evaluated at a given time  , applied on a state vector and combined with other Tridiagonal instances using algebraic operations.
, applied on a state vector and combined with other Tridiagonal instances using algebraic operations.
Tridiagonal internally bookkeeps to which time instant its state corresponds.
Policy of storing diagonals: only the non-zeros. Policy of storing frequencies: either none or all of them. Because of these policies, Tridiagonal can represent a diagonal matrix without significant overhead.
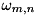 are not necessarily real here, Tridiagonal works also for non-Hermitian operators. On non-unitary transformations in quantum mechanics cf. these notes.
are not necessarily real here, Tridiagonal works also for non-Hermitian operators. On non-unitary transformations in quantum mechanics cf. these notes.| RANK | arity of the Hilbert space corresponding to 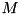 above above |
![\[H\Int(t)=\bigotimes_{m=0}^{M-1}\sum_{i_m\in\mathbb{K}_m}\sum_{n_m=0}^{N_m-1-i_m}e^{\delta^{i_m}_{m,n}t}\alpha^{i_m}_{m,n}\ket{n_m+i_m}\bra{n_m},\]](form_161.png)
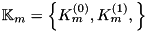 an arbitrary set, and
an arbitrary set, and  .
. Definition at line 103 of file Tridiagonal.h.
|
explicit |
Constructor for unary Tridiagonal.
This is the principal way to create an object of this class, which can be used in the unary case only, as ensured by the trailing dummy argument. This creates an object corresponding to the elementary operator
![\[H^\text{elem}/i=\sum_{n=0}^{N-1}\alpha^{(0)}_n\ket{n}\bra{n}+\sum_{n=0}^{N-1-K}\lp\alpha^{(-)}_n\ket{n+K}\bra{n}+\alpha^{(+)}_n\ket{n}\bra{n+K}\rp\]](form_167.png)
when toFreq=false and
![\[H\Int^\text{elem}(t=0)/i=\sum_{n=0}^{N-1-K}\lp e^{\delta_{n}t}\alpha^{(-)}_n\ket{n+K}\bra{n}+e^{-\delta_{n}t}\alpha^{(+)}_n\ket{n}\bra{n+K}\rp\]](form_168.png)
when toFreq=true. In this case, the  frequencies are calculated out of
frequencies are calculated out of 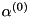 as
as 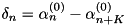 .
.
Either of the three initializing arrays might be zero-size, which signifies that the corresponding diagonal is zero, however, if they are nonzero-size, then their sizes must be compatible with each other. If both minus and plus are zero-size (purely diagonal matrix), then k might be zero as well. Violation is detected at runtime, and an exception of type TridiagonalConsistencyErrorException is thrown.
k should be considered a compile-time or a runtime parameter. In the majority of cases it is known already an compile time (e.g. ladder operators, angular momentum operators, etc.). The reason why it is treated as a runtime parameter is spatial degrees of freedom. There, operators like  ,
,  , etc., are also tridiagonal in momentum space, and we wanted to have to possibility of specifying
, etc., are also tridiagonal in momentum space, and we wanted to have to possibility of specifying  at runtime.
at runtime. | zero | corresponds to 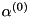 |
| k | corresponds to 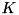 above above |
| minus | corresponds to 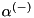 |
| plus | corresponds to 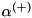 |
| toFreqs | governs whether the main diagonal ( 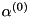 ) is converted to frequencies ) is converted to frequencies 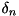 |
| quantumoperator::Tridiagonal< RANK >::Tridiagonal | ( | const Tridiagonal< RANK2 > & | , |
| const Tridiagonal< RANK-RANK2 > & | |||
| ) |
Constructs the object as the direct product of two Tridiagonal matrices.
This is rather non-trivial, and the calculation of the resulting diagonals’ position is at the moment calculated at runtime, though it could partly be done at compile time. The eventual frequencies are also composed, direct product translates to a “direct sum” in this case. This really makes sense only if the time instants of the two tridiagonals are the same. Violation is detected at runtime, and an exception of type TridiagonalTimeMismatchException is thrown.
All tridiagonals of RANK>1 in the framework originate from direct products of unary tridiagonals.
| RANK2 | the arity of one of the arguments (the other being RANK-RANK2) |
| void quantumoperator::Tridiagonal< RANK >::apply | ( | const StateVectorLow & | psi, |
| StateVectorLow & | dpsidt | ||
| ) | const |
“Applies” the tridiagonal matrix on the state vector psiprime, in the vein of structure::Hamiltonian::addContribution(), that is 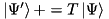 .
.
Finding out which of the 3 to the power of arity diagonals corresponds to which state-vector slice when “applying”, is a formidable task for higher arity, and a significant portion of this calculation is done at compile time. The structure of this problem naturally maps to a recursion. There are 2 possibilities:
quantumoperator/applyImpl/generate.py for each RANK (the Python script takes the rank as its first parameter in the command line). The user is encouraged to try it out to see the structure of the problem. Here, the recursion inherent in the problem is shifted to this Python script. This solution sidesteps template metaprogramming, however, it has the drawback that the amount of code such produced grows exponentially with the arity. This possibility is used if the DO_CONSIDER_EXPLICITLY_SPECIALIZED_TRIDIAGONAL_APPLIES macro is defined @ compilation.| const dcomp quantumoperator::Tridiagonal< RANK >::average | ( | const quantumdata::LazyDensityOperator< RANK > & | , |
| const typename quantumdata::LazyDensityOperator< RANK >::Idx & | , | ||
| IntRANK | = _1_ |
||
| ) |
Calculates the quantum average of a Tridiagonal in a quantum state described by a (unary) quantumdata::LazyDensityOperator.
| Tridiagonal& quantumoperator::Tridiagonal< RANK >::furnishWithFreqs | ( | const Diagonal & | mainDiagonal, |
| IntRANK | = _1_ |
||
| ) |
Furnishes a unary tridiagonal with frequencies calculated from mainDiagonal.
Note that the matrix may have its own main diagonal in this case, which remains untouched. (This is actually exploited if we want to transform out only part of a main diagonal with interaction picture.)
*this| const Tridiagonal quantumoperator::Tridiagonal< RANK >::hermitianConjugate | ( | ) | const |
Returns a newly constructed object, which is the Hermitian conjugate of this.
Transposition involves a non-trivial permutation of diagonals, which could be done @ compile-time, but at the moment it’s runtime.
Frequencies need not be transposed, because they are identical to their transpose.
| Tridiagonal& quantumoperator::Tridiagonal< RANK >::operator+= | ( | const Tridiagonal< RANK > & | ) |
Naive addition.
The structures of the two objects must match, and there is a rather complicated set of rules as to what is meant by “matching”:
ks must match.Any violation of these rules is detected at runtime, and an exception of type TridiagonalStructureMismatchException is thrown.
| Tridiagonal& quantumoperator::Tridiagonal< RANK >::propagate | ( | double | t | ) |
Updates the elements of the matrix to time instant t using the stored frequencies.
*this
|
related |
A free-standing version of Tridiagonal::apply.
|
related |
Same as Tridiagonal::furnishWithFreqs, but returns a copy of its first argument furnished with frequencies.
| tridiag | Tridiagonal whose copy is to be furnished with frequencies |
| mainDiagonal | main diagonal determining the frequencies to be used for furnishing |
|
related |
Unary identity operator as a Tridiagonal.
|
related |
Direct product.
Definition at line 338 of file Tridiagonal.h.
|
related |
|
related |
Returns the anti-Hermitian operator  .
.
Definition at line 348 of file Tridiagonal.h.
|
related |
Returns the Hermitian operator 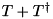 .
.
Definition at line 355 of file Tridiagonal.h.
|
related |
Returns the anti-Hermitian operator 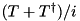 .
.
Definition at line 362 of file Tridiagonal.h.
|
related |
Unary zero operator as a Tridiagonal.