The interface every system having Liouvillean time-evolution must present towards the trajectory drivers. More...
#include <Liouvillean.h>
 Inheritance diagram for structure::Liouvillean< RANK >:
Inheritance diagram for structure::Liouvillean< RANK >: Collaboration diagram for structure::Liouvillean< RANK >:
Collaboration diagram for structure::Liouvillean< RANK >:Public Types | |
| typedef boost::shared_ptr< const Liouvillean > | Ptr |
| typedef quantumdata::StateVector< RANK > | StateVector |
| typedef Base::StateVectorLow | StateVectorLow |
| typedef Base::DensityOperatorLow | DensityOperatorLow |
| typedef Base::LazyDensityOperator | LazyDensityOperator |
| typedef Base::DArray1D | Rates |
| The 1D real array for storing the jump rates. | |
 Public Types inherited from quantumdata::Types< RANK, LiouvilleanAveragedCommonRanked< RANK > > Public Types inherited from quantumdata::Types< RANK, LiouvilleanAveragedCommonRanked< RANK > > | |
| typedef CArray< RANK > | StateVectorLow |
| typedef CArray< 2 *RANK > | DensityOperatorLow |
Public Member Functions | |
| const Rates | rates (double t, const StateVector &psi) const |
Returns the set of jump rates 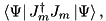 where the Lindblads are in general time-dependent. More... where the Lindblads are in general time-dependent. More... | |
| void | actWithJ (double t, StateVectorLow &psi, size_t m) const |
Performs the quantum jump operation 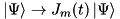 . More... . More... | |
Static Public Attributes | |
| static const int | N_RANK =RANK |
The interface every system having Liouvillean time-evolution must present towards the trajectory drivers.
The time-evolution must be Markovian where the Lindblad form of the Master equation is the most general one possible:
![\[\dot\rho=\frac1{i\hbar}\comm{H}\rho+\sum_m\lp J_m\rho J_m^\dag-\frac12\comm{J_m^\dag J_m}{\rho}_+\rp\]](form_193.png)
The class represents the set of 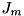 operators (Lindblads or quantum jump operators) of arbitrary number, either for Master equation or Monte Carlo wave-function evolution (in the latter case it calculates the jump rates as well).
operators (Lindblads or quantum jump operators) of arbitrary number, either for Master equation or Monte Carlo wave-function evolution (in the latter case it calculates the jump rates as well).
| RANK | arity of the Hilbert space |
Definition at line 37 of file Liouvillean.h.
|
inline |
Performs the quantum jump operation 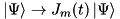 .
.
| [in] | t |  |
| [in,out] | psi |  |
| [out] | m | 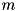 |
Definition at line 64 of file Liouvillean.h.
|
inline |
Returns the set of jump rates 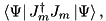 where the Lindblads are in general time-dependent.
where the Lindblads are in general time-dependent.
Simply redirects to LiouvilleanAveragedCommonRanked::average, so that this function does not appear in the interface for implementers.
Definition at line 61 of file Liouvillean.h.