The Master equation for the evolution of a density operator reads
![\[\dot\rho=\frac1{i\hbar}\comm{H}{\rho}+\sum_m\lp{J_m\rho{J_m^\dag}-\frac12\comm{J_m^\dag J_m}{\rho}_+}\rp\equiv\frac1{i\hbar}\lp\HnH\,\rho-\rho\HnH^\dag\rp+\sum_mJ_m\rho{J_m^\dag}=2\Re\lbr\frac\HnH{i\hbar}\rho\rbr+\sum_mJ_m\lp{J_m\rho}\rp^\dag,\]](form_67.png)
where, after the second equality, the non-Hermitian “Hamiltonian” is defined as (cf. Description of the MCWF method)
![\[\HnH=H-\frac{i\hbar}2\sum_m J^\dag_m J_m.\]](form_36.png)
Since both the Hamiltonian and Lindblad operators are expressed in a finite discrete basis, this is simply an ODE evolution.
Since each Hamiltonian and/or lossy physical system in the framework provides services to calculate the effect of  (cf. structure::Hamiltonian::addContribution) and the jumps
(cf. structure::Hamiltonian::addContribution) and the jumps 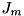 (cf. structure::Liouvillean::actWithJ) on state vectors, these being indispensable for the Monte Carlo wave-function method, no separate services are needed to calculate Master-equation evolution for these systems.
(cf. structure::Liouvillean::actWithJ) on state vectors, these being indispensable for the Monte Carlo wave-function method, no separate services are needed to calculate Master-equation evolution for these systems.
The steps are as follows:
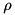 to get
to get  .
.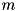 :
: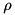 and iterate through its columns to get
and iterate through its columns to get  .
.The drawback of this method is that it necessitates a temporary copy of the full density operator. Alternatively, systems may provide specialized code to calculate 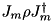 directly, hence circumventing steps (a)-(b)-(a).
directly, hence circumventing steps (a)-(b)-(a).
Consider these notes, whose notation we adopt. It is easy to see that a density-operator evolution of the form
![\[\dot\rho_T=2\Re\lbr\mathcal{A}^T\rho_T\rbr+\sum_mJ_m^T\rho_T\lp J_m^T\rp^\dag\]](form_75.png)
can always be unravelled up to first order in  via an MCWF-like two-step stochastic process as:
via an MCWF-like two-step stochastic process as:
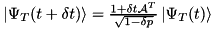 , with probability
, with probability 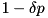 .
.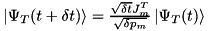 , with probability
, with probability  for either
for either 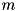 , such that
, such that 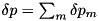 .
.If we require that the second possibility do not alter the norm, as in the case of the MCWF method (the first may in the case when  is non-Hermitian), that is, if the norm may change only in time (jumps considered instantaneous), then we get the further requirement that
is non-Hermitian), that is, if the norm may change only in time (jumps considered instantaneous), then we get the further requirement that 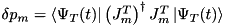 .
.
This shows that the Master driver will only work correctly if
![\[J_m^T\rho\lp J_m^T\rp^\dag=J_m\rho J_m^\dag\quad\forall\rho,\;m,\]](form_83.png)
because structure::Liouvillean::actWithJ calculates the latter, while quantumtrajectory::Master expects the former.
The requirement for the applicability of the quantumtrajectory::Master driver might seem formidable, but the situation is actually not so bad. First of all, the problem does not arise at all for systems that do not inherit from structure::Exact.
Consider a harmonic-oscillator mode in some rotating frame, as in this Section. Here, the transformation operator reads 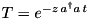 , and the transformed jump operators:
, and the transformed jump operators:  , which makes that in the case of a purely imaginary
, which makes that in the case of a purely imaginary 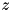 , which is the case for a purely rotating (and not shrinking) frame, the requirement is fulfilled.
, which is the case for a purely rotating (and not shrinking) frame, the requirement is fulfilled.