This Guide describes the use of the set of tools in C++QED aimed at the implementation of new elements representing elementary free physical systems and their interactions. These tools are found in two namespaces:
- structure: this namespace comprises classes wherefrom all elements must be derived to present the necessary interfaces to trajectory drivers (cf. the quantumtrajectory namespace)
- quantumoperator: here, such operator classes are found that represent special operator structures ubiquitous in atomic, molecular, and optical physics.
This set of tools constitutes the Level-2 interface of C++QED, below Level-1, which is the interface for writing scripts from already available elements (cf. userguide).
- Note
- The files referred to in this Section are found in directory
examples in the distribution. The code examples are expected to compile, cf. examples/Jamfile.
Implementation of a class representing a harmonic-oscillator mode
We demonstrate how to implement an element representing a pumped lossy mode in a truncated Fock space. In the frame rotating with the pump frequency, it is described by the Hamiltonian:
![\[H=-\delta a^\dagger a+\lp\eta a^\dagger+\hermConj\rp,\]](form_0.png)
where  is the detuning between the oscillator and the pump frequencies. The Liouvillean:
is the detuning between the oscillator and the pump frequencies. The Liouvillean:
![\[\Liou\rho=\kappa\lp(n_\text{Th}+1)\lp2a\rho a^\dagger-\comm{a^\dagger a}{\rho}_+\rp+n_\text{Th}\lp2a^\dagger\rho a-\comm{a\,a^\dagger}{\rho}_+\rp\rp\]](form_2.png)
The frequency-like parameters are  ,
, 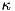 , and
, and 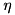 , representing the mode frequency, loss rate, and pumping Rabi frequency, respectively. A dimensionless parameter is
, representing the mode frequency, loss rate, and pumping Rabi frequency, respectively. A dimensionless parameter is 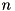 (the average number of thermal photons in the heat bath) and the cutoff of the Fock space.
(the average number of thermal photons in the heat bath) and the cutoff of the Fock space.
Using the notation of Sec. Description of the MCWF method
![\[J_0=\sqrt{2\kappa(n_\text{Th}+1)}a,\quad J_1=\sqrt{2\kappa n_\text{Th}}a^\dagger.\]](form_6.png)
The non-Hermitian Hamiltonian for the Monte Carlo wave-function method reads:
![\[\HnH=\lp-\delta-i\kappa(2n_\text{Th}+1)\rp a^\dagger a+\lp\eta a^\dagger+\hermConj\rp\equiv-iz\,a^\dagger a+\lp\eta a^\dagger+\hermConj\rp,\]](form_7.png)
where we have introduced the complex frequency
![\[z\equiv\kappa(2n_\text{Th}+1)-i\delta.\]](form_8.png)
The element has to be represented by a class which inherits publicly from the necessary classes in the structure namespace. In this simple case, it is basically two helper functions returning quantumoperator::Tridiagonal instances, a constructor, and two virtual functions inherited from structure::ElementAveraged that have to be written.
- See also
- The description of quantumoperator::Tridiagonal
Consider the file ExampleMode.h:
using namespace freesystem;
namespace basic {
class PumpedLossyMode
{
public:
PumpedLossyMode(
double delta,
double kappa,
dcomp eta,
double nTh,
size_t cutoff);
private:
const Averages average_v(
NoTime,
const LazyDensityOperator&)
const;
};
}
inline const Tridiagonal aop(
const basic::PumpedLossyMode& mode) {
return aop(mode.getDimension());}
Though the structure::NoTime tagging class as a function argument creates some redundancy, it is necessary because of the design of the structure-bundle. Note that structure::ElementLiouvilleanStrategies (like structure::ElementLiouvillean) assumes that the number of Lindblads is known @ compile time, as is the case here. If this is not the case, structure::Liouvillean has to be used instead.
This will suffice here. Let us look at the implementations in ExampleMode.cc:
1 // Copyright András Vukics 2006–2014. Distributed under the Boost Software License, Version 1.0. (See accompanying file LICENSE.txt)
2 #include "ExampleMode.h"
4 #include "ElementLiouvillean.tcc"
5 #include "Tridiagonal.tcc"
6 #include "TridiagonalHamiltonian.tcc"
8 #include <boost/bind.hpp>
13 void aJump (StateVectorLow&, double kappa_nPlus1);
14 void aDagJump(StateVectorLow&, double kappa_n );
16 double aJumpRate (const LazyDensityOperator&, double kappa_nPlus1);
17 double aDagJumpRate(const LazyDensityOperator&, double kappa_n );
20 basic::PumpedLossyMode::PumpedLossyMode(double delta, double kappa, dcomp eta, double nTh, size_t cutoff)
23 CF{"(kappa*(2*nTh+1),delta)",dcomp(kappa*(2*nTh+1),delta), cutoff },
24 CF{"eta" ,eta ,sqrt(cutoff)}
We construct the
structure::Free base with the dimension of the system and the name-value-multiplier tuples for the frequency-like parameters of the system, which in this case are all complex (cf. the explanation @
structure::DynamicsBase). We use C++11 initializer lists and the
structure::DynamicsBase::CF typedef.
1 TridiagonalHamiltonian<1,false>(dcomp(-kappa*(2*nTh+1),delta)*nop(cutoff)
3 tridiagPlusHC_overI(conj(eta)*aop(cutoff))),
We construct the time-independent
quantumoperator::TridiagonalHamiltonian base. This is greatly facilitated by the algebra and helpers of the
quantumoperator::Tridiagonal class.
- Warning
- When implementing the Hamiltonian, not
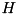 itself but
itself but 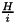 has to supplied!
has to supplied!
1 ElementLiouvilleanStrategies<1,2>(JumpStrategies(bind(aJump ,_1,kappa*(nTh+1)),
2 bind(aDagJump,_1,kappa* nTh )),
3 JumpRateStrategies(bind(aJumpRate ,_1,kappa*(nTh+1)),
4 bind(aDagJumpRate,_1,kappa* nTh )),
5 "Mode",{"photon loss","photon absorption"}),
We construct the
structure::ElementLiouvilleanStrategies base, whose second template argument denotes the number of different quantum jumps, which is 2 in this case. The constructor takes the strategies for calculating the impact of a jump on a
structure::freesystem::StateVectorLow, and for calculating the rate from a
structure::freesystem::LazyDensityOperator. These strategy functions are produced from the free-standing helpers in Lines 10-14 above through argument binding. The strategies are followed by a description of the lossy element and the decay channels. The number of descriptive labels must agree with the number of strategies.
1 ElementAveraged<1>("PumpedLossyMode",{"<number operator>","real(<ladder operator>)","imag(\")"})
We construct the
structure::ElementAveraged base, with parameters necessary to produce a simple key of the quantum averages that are communicated towards the user. Here we calculate only three such averages, the expectation value of the number operator, and the real and imaginary parts of that of the ladder operator.
2 getParsStream()<<"# Pumped lossy mode";
With the
structure::DynamicsBase::getParsStream function we obtain a stream whereon we can write more information about the object that gets communicated towards the user in that part of the output which summarizes the parameters of the actual run.
Next, the inherited function structure::Averaged::average is implemented (according to the non-virtual interface idiom, its virtual counterpart is called average_v):
1 auto basic::PumpedLossyMode::average_v(NoTime, const LazyDensityOperator& matrix) const -> const Averages
3 auto averages(initializedAverages());
5 averages(0)=aJumpRate(matrix,1);
the expectation value of the photon number is calculated (where we can reuse our function
aJumpRate, with unit loss rate).
2 for (int n=1; n<int(matrix.getDimension()); n++) {
4 dcomp offdiag(matrix(n)(n-1));
5 averages(1)+=sqrtn*real(offdiag);
6 averages(2)+=sqrtn*imag(offdiag);
the expectation value of the ladder operator is calculated (real & imaginary parts)
The implementation of the helpers is also quite straightforward. It may come to a separate file ExampleModeImpl.cc:
1 // Copyright András Vukics 2006–2014. Distributed under the Boost Software License, Version 1.0. (See accompanying file LICENSE.txt)
2 #include "ExampleMode.h"
3 #include "Tridiagonal.tcc"
5 void aJump (StateVectorLow& psi, double kappa_nPlus1)
7 double fact=sqrt(2.*kappa_nPlus1);
8 int ubound=psi.ubound(0);
9 for (int n=0; n<ubound; ++n)
10 psi(n)=fact*sqrt(n+1)*psi(n+1);
15 void aDagJump(StateVectorLow& psi, double kappa_n )
17 double fact=sqrt(2.*kappa_n);
18 for (int n=psi.ubound(0); n>0; --n)
19 psi(n)=fact*sqrt(n)*psi(n-1);
26 double photonNumber(const LazyDensityOperator& matrix)
29 for (size_t n=1; n<matrix.getDimension(); ++n)
37 double aJumpRate (const LazyDensityOperator& matrix, double kappa_nPlus1)
39 return 2.*kappa_nPlus1*photonNumber(matrix);
43 double aDagJumpRate(const LazyDensityOperator& matrix, double kappa_n )
45 return 2.*kappa_n*(photonNumber(matrix)+matrix.trace());
49 const Tridiagonal aop(size_t dim)
51 typedef Tridiagonal::Diagonal Diagonal;
52 Diagonal diagonal(dim-1);
53 return Tridiagonal(Diagonal(),1,Diagonal(),diagonal=sqrt(blitz::tensor::i+1.));
- Warning
- In situations like this, it is extremely important to write
blitz::tensor::i+1., otherwise the blitz::sqrt function will operate within the integers, which is perhaps a shortcoming of the Blitz++ library in this respect.
4 const Tridiagonal::Diagonal mainDiagonal(const dcomp& z, size_t dim)
6 Tridiagonal::Diagonal res(dim);
12 const Tridiagonal nop(size_t dim)
2 return Tridiagonal(mainDiagonal(1.,dim));
Exploiting interaction picture
In many situations, it pays to transfer to interaction picture defined by the first term of the Hamiltonian 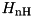 above. The ladder operator in interaction picture is
above. The ladder operator in interaction picture is
![\[a\Int(t)=a e^{-zt},\]](form_12.png)
so that the Hamiltonian reads
![\[H\Int(t)=\lp\eta a^\dagger e^{zt}+\eta^*ae^{-zt}\rp.\]](form_13.png)
- See also
- These notes on how to treat interaction pictures defined by non-unitary transition operators in a consistent way.
In this case, the class representing the element has to be derived from structure::Exact as well, which provides an interface allowing for the transformation between the two pictures. In addition, instead of quantumoperator::TridiagonalHamiltonian <1,false>, we need to derive from quantumoperator::TridiagonalHamiltonian <1,true> because the Hamiltonian is now time-dependent.
- Note
- In general usage, the jump and the averages are calculated in the normal picture also in this case (cf. explanation of classes structure::Hamiltonian, structure::Exact, structure::Liouvillean, and structure::Averaged, and furthermore quantumtrajectory::MCWF_Trajectory). This allows for reusing the same code in both pictures. (Incidentally, here the Liouvillean remains unchanged anyway.)
1 #include "FreeExact.h" // Further inculdes and using directives the same as above
6 class PumpedLossyModeIP
7 : public Free, public FreeExact<false>, public TridiagonalHamiltonian<1,true>, public ElementLiouvilleanStrategies<1,2>, public ElementAveraged<1>
10 typedef ElementAveraged<1>::LazyDensityOperator LazyDensityOperator;
12 PumpedLossyModeIP(double delta, double kappa, dcomp eta, double nTh, size_t cutoff);
14 const dcomp get_z() const {return z_;}
17 void updateU(OneTime) const;
19 bool applicableInMaster_v() const {return true;}
21 const Averages average_v(NoTime, const LazyDensityOperator&) const;
23 const dcomp z_; // Needed for updateU
The
structure::OneTime tagging class at the same time carries the information about the time instant to which the (diagonal) transformation operator has to be updated.
structure::OneTime can be implicitly converted into a double.
In the implementation, the only difference from the previous case will be the constructor, because the Hamiltonian now also requires furnishing with frequencies (cf. quantumoperator::furnishWithFreqs), and the implementation of the virtual function structure::FreeExact::updateU.
- Note
- In connection with the structure::Exact::applicableInMaster virtual function implemented here, cf. also this note.
When “furnished with frequencies”, a quantumoperator::Tridiagonal object will internally take care about the time-dependent phases appearing in 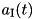 and
and 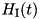 :
:
1 const Tridiagonal::Diagonal mainDiagonal(const dcomp& z, size_t cutoff);
4 basic::PumpedLossyModeIP::PumpedLossyModeIP(double delta, double kappa, dcomp eta, double nTh, size_t cutoff)
7 RF{"kappa*(2*nTh+1)",kappa*(2*nTh+1),cutoff},
10 CF{"eta",eta,sqrt(cutoff)}),
11 FreeExact<false>(cutoff),
12 TridiagonalHamiltonian<1,true>(furnishWithFreqs(tridiagPlusHC_overI(conj(eta)*aop(cutoff)),
13 mainDiagonal(dcomp(kappa*(2*nTh+1),-delta),cutoff))),
14 ElementLiouvilleanStrategies<1,2>(JumpStrategies(bind(aJump ,_1,kappa*(nTh+1)),
15 bind(aDagJump,_1,kappa* nTh )),
16 JumpRateStrategies(bind(aJumpRate ,_1,kappa*(nTh+1)),
17 bind(aDagJumpRate,_1,kappa* nTh )),
18 "Mode",{"photon loss","photon absorption"}),
19 ElementAveraged<1>("PumpedLossyMode",{"<number operator>","real(<ladder operator>)","imag(\")"}),
20 z_(kappa*(2*nTh+1),-delta)
24 void basic::PumpedLossyModeIP::updateU(OneTime dtDid) const
26 getDiagonal()=exp(-z_*(dtDid*blitz::tensor::i));
30 // PumpedLossyModeIP::average_v exactly the same as PumpedLossyMode::average_v above
assumes that the operator transforming between the two pictures is diagonal, and the factors to update are simply its diagonal elements. If this is not the case, Exact has to be used instead. Here, since there are also real frequency-like parameters, we have to use
structure::DynamicsBase::RF as well.
- Note
- Since a lot of the code from the previous case can be reused here, one will usually adopt an inheritence- or class-composition-based solution to implement classes like
PumpedLossyMode and PumpedLossyModeIP (for an inheritance-based solution, cf. below; for one based on class-composition, cf. the actual implementation of a harmonic-oscillator mode in the framework in elements/frees/Mode_.h).
Implementing an X-X interaction
Let us consider the interaction described by the Hamiltonian
![\[H_\text{X-X}=g(a+a^\dagger)(b+b^\dagger).\]](form_16.png)
The class implementing this interaction has to be derived from structure::Interaction <2> because it is a binary interaction, and quantumoperator::TridiagonalHamiltonian <2,...> (note that quantumoperator::Tridiagonal is capable to represent direct products of tridiagonal matrices in the case of RANK>1).
The only thing requiring some care is that once we transform some elements into interaction picture, the whole Hamiltonian is transformed, that is, 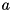 or
or 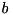 or both may be in interaction picture. Here, for the sake of simplicity, we assume that both constituents are of the type
or both may be in interaction picture. Here, for the sake of simplicity, we assume that both constituents are of the type PumpedLossyMode. Hence, the Hamiltonian is in fact
![\[H_{\text{X-X;I}}(t)=g(ae^{-z_at}+a^\dagger e^{z_at})(be^{-z_bt}+b^\dagger e^{z_bt}).\]](form_19.png)
Consider ExampleInteraction.h:
1 #include "ExampleMode.h"
3 #include "Interaction.h"
4 #include "TridiagonalHamiltonian.tcc"
5 #include "StateVector.tcc"
10 : public Interaction<2>, public TridiagonalHamiltonian<2,false>
13 InteractionX_X(const PumpedLossyMode&, const PumpedLossyMode&, double g);
ExampleInteraction.cc then reads
1 #include "ExampleInteraction.h"
3 basic::InteractionX_X::InteractionX_X(const PumpedLossyMode& m0, const PumpedLossyMode& m1, double g)
4 : Interaction<2>(m0,m1,RF{"g",g,sqrt(m0.getDimension()*m1.getDimension())}),
5 TridiagonalHamiltonian<2,false>(g*
6 (aop(m0)+aop(m0).dagger())*
7 (aop(m1)+aop(m1).dagger())
As we see, the Hamiltonian can be written in a rather straightforward way, and it internally takes care about the time-dependent phases appearing in
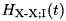
, which result from the use of interaction picture.
The free elements are stored as shared pointers in the interaction element, and the constant references supplied to the constructor are turned into (non-owning) shared pointers (cf. cpputils::sharedPointerize). Of course, the free elements have to live in a larger scope than the interaction, otherwise we may run into trouble with dangling pointers.
Using class inheritance
For an inheritance-based solution, it pays to define a base class collecting all the common services. Consider the following snippet from ExampleMode.h:
1 namespace hierarchical {
3 // All inculdes and using directives the same as above
5 class ModeBase : public Free, public ElementLiouvillean<1,2>, public ElementAveraged<1>
8 typedef ElementLiouvillean<1,2>::StateVectorLow StateVectorLow ;
9 typedef ElementAveraged<1>::LazyDensityOperator LazyDensityOperator;
12 ModeBase(double kappa, double nTh, size_t cutoff);
15 void doActWithJ(NoTime, StateVectorLow&, LindbladNo<0>) const;
16 void doActWithJ(NoTime, StateVectorLow&, LindbladNo<1>) const;
18 double rate(NoTime, const LazyDensityOperator&, LindbladNo<0>) const;
19 double rate(NoTime, const LazyDensityOperator&, LindbladNo<1>) const;
21 const Averages average_v(NoTime, const LazyDensityOperator&) const;
23 const double kappa_, nTh_; // needed for calculating jumps & rates
Here, instead of
structure::ElementLiouvilleanStrategies, we can rather use
structure::ElementLiouvillean, which has as many virtual functions
doActWithJ and
rate as there are jumps (indicated by the second template argument), distinguished by the tagging classes
structure::lindblad::Base::LindbladNo. It results in a compile-time error to instantiate such a class with an argument not smaller than the number of Lindblads (since the numbering of jumps begins with 0). Via this solution we can get around the awkwardness of specifying the jump and rate strategies for
structure::ElementLiouvilleanStrategies, while retaining a way of controlling the number of Lindblads @ compile time.
Deriving from ModeBase, the definition of PumpedLossyMode is trivial, while for PumpedLossyModeIP, we have to define the virtual functions inherited from structure::FreeExact:
1 namespace hierarchical {
5 : public ModeBase, public TridiagonalHamiltonian<1,false>
8 PumpedLossyMode(double delta, double kappa, dcomp eta, double nTh, size_t cutoff);
13 class PumpedLossyModeIP
14 : public ModeBase, public FreeExact<false>, public TridiagonalHamiltonian<1,true >
17 PumpedLossyModeIP(double delta, double kappa, dcomp eta, double nTh, size_t cutoff);
19 const dcomp get_z() const {return z_;}
22 void updateU(OneTime) const;
24 bool applicableInMaster_v() const {return true;}
26 const dcomp z_; // Needed for updateU
- Note
- The correct treatment of frequency-like parameters would require more care in this case, since
ModeBase does not know about delta & eta
The implementations come in ExampleMode.cc:
1 hierarchical::ModeBase::ModeBase(double kappa, double nTh, size_t cutoff)
2 : Free(cutoff,RF{"kappa*(2*nTh+1)",kappa*(2*nTh+1),cutoff}),
3 ElementLiouvillean<1,2>("Mode",{"photon loss","photon absorption"}),
4 ElementAveraged<1>("PumpedLossyMode",{"<number operator>","real(<ladder operator>)","imag(\")"}),
5 kappa_(kappa), nTh_(nTh)
9 void hierarchical::ModeBase::doActWithJ(NoTime, StateVectorLow& psi, LindbladNo<0>) const
11 aJump(psi,kappa_*(nTh_+1));
14 void hierarchical::ModeBase::doActWithJ(NoTime, StateVectorLow& psi, LindbladNo<1>) const
16 aDagJump(psi,kappa_*nTh_);
19 double hierarchical::ModeBase::rate(NoTime, const LazyDensityOperator& matrix, LindbladNo<0>) const
21 return aJumpRate(matrix,kappa_*(nTh_+1));
24 double hierarchical::ModeBase::rate(NoTime, const LazyDensityOperator& matrix, LindbladNo<1>) const
26 return aDagJumpRate(matrix,kappa_*nTh_);
29 // ModeBase::average_v exactly the same as PumpedLossyMode::average_v above
and the derived classes:
1 hierarchical::PumpedLossyMode::PumpedLossyMode(double delta, double kappa, dcomp eta, double nTh, size_t cutoff)
2 : ModeBase(kappa,nTh,cutoff),
3 TridiagonalHamiltonian<1,false>(dcomp(-kappa*(2*nTh+1),delta)*nop(cutoff)
5 tridiagPlusHC_overI(conj(eta)*aop(cutoff)))
9 hierarchical::PumpedLossyModeIP::PumpedLossyModeIP(double delta, double kappa, dcomp eta, double nTh, size_t cutoff)
10 : ModeBase(kappa,nTh,cutoff),
11 FreeExact<false>(cutoff),
12 TridiagonalHamiltonian<1,true>(furnishWithFreqs(tridiagPlusHC_overI(conj(eta)*aop(cutoff)),
13 mainDiagonal(dcomp(kappa*(2*nTh+1),-delta),cutoff))),
14 z_(kappa*(2*nTh+1),-delta)
18 // PumpedLossyModeIP::updateU exactly the same as above
We may define a function using runtime-dispatching for a ladder operator either furnished or not furnished with frequencies, depending on the actual type. It should be implemented via dynamic casting:
1 const Tridiagonal aop(const hierarchical::ModeBase& mode)
3 using namespace hierarchical;
4 size_t dim=mode.getDimension();
5 if (const auto modeIP=dynamic_cast<const PumpedLossyModeIP*>(&mode))
6 return furnishWithFreqs(aop(dim),mainDiagonal(modeIP->get_z(),dim));
Interaction element in the inheritance-based design
Based on the above design of the mode-element and the dispatching ladder-operator function, we may define an interaction element that works correctly with either free element, if the constructor expects arguments of type ModeBase:
1 namespace hierarchical {
4 : public Interaction<2>, public TridiagonalHamiltonian<2,true>
7 InteractionX_X(const ModeBase&, const ModeBase&, double g);
The implementation is formally equivalent to the previous:
1 hierarchical::InteractionX_X::InteractionX_X(const ModeBase& m0, const ModeBase& m1, double g)
2 : Interaction<2>(m0,m1,RF{"g",g,sqrt(m0.getDimension()*m1.getDimension())}),
3 TridiagonalHamiltonian<2,true>(g*
4 (aop(m0)+aop(m0).dagger())*
5 (aop(m1)+aop(m1).dagger())
- Warning
- Here, it would cause a hard-to-detect physical error to use quantumoperator::TridiagonalHamiltonian
<2,false> instead of quantumoperator::TridiagonalHamiltonian <2,true>, because in the former case, the time update of the binary tridiagonal would not occur even with PumpedLossyModeIP.
Other uses of interaction elements
In the language of the framework, every element that operates on more than one quantum numbers is an interaction.
Hence, if we need for instance an element calculating correlations between two free subsystems (or, two quantum numbers in general), it has to be derived from Interaction because only an interaction element has a chance to access more than quantum numbers.
Assume we need an element calculating the dynamics of an X-X interaction between two modes as above, but it also lets the user monitor the correlations 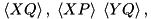 and
and 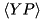 between the modes, where
between the modes, where 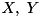 and
and 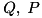 are the quadratures of the two modes, respectively. The element can be derived from the former interaction element in the inheritance-based design:
are the quadratures of the two modes, respectively. The element can be derived from the former interaction element in the inheritance-based design:
1 namespace hierarchical {
3 class InteractionX_X_Correlations : public InteractionX_X, public ElementAveraged<2>
6 InteractionX_X_Correlations(const ModeBase& m0, const ModeBase& m1, double g)
7 : InteractionX_X(m0,m1,g),
8 ElementAveraged<2>("ModeCorrelations",{"<XQ>","<XP>","<YQ>","<YP>"})
12 const Averages average_v(NoTime, const LazyDensityOperator&) const;
Since now we need to operate on two quantum numbers to calculate the quantum averages, we derived from
structure::ElementAveraged <2>, which operates on a binary
quantumdata::LazyDensityOperator. The implementation of the averaging function may read
1 auto hierarchical::InteractionX_X_Correlations::average_v(NoTime, const LazyDensityOperator& matrix) const -> const Averages
3 auto averages(initializedAverages());
5 for (int n=0; n<int(matrix.getDimension(0)); n++) for (int m=1; m<int(matrix.getDimension(1)); m++) {
6 if(n<int(matrix.getDimension(0))-1) {
7 dcomp temp=sqrt(m*(n+1))*matrix(n,m)(n+1,m-1);
8 averages(0)+=real(temp);
9 averages(1)+=imag(temp);
12 dcomp temp=sqrt(m*n)*matrix(n,m)(n-1,m-1);
13 averages(2)+=real(temp);
14 averages(3)+=imag(temp);
at this point, the
averages array contains the real and imaginary parts of
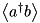
and
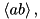
respectively.
Now the desired set of quantum averages can be obtained via linear operations:
3 xq= averages(0)+averages(2),
4 xp= averages(1)+averages(3),
5 yq=-averages(1)+averages(3),
6 yp= averages(0)-averages(2);
![\[H=-\delta a^\dagger a+\lp\eta a^\dagger+\hermConj\rp,\]](form_0.png)
 is the detuning between the oscillator and the pump frequencies. The Liouvillean:
is the detuning between the oscillator and the pump frequencies. The Liouvillean: ![\[\Liou\rho=\kappa\lp(n_\text{Th}+1)\lp2a\rho a^\dagger-\comm{a^\dagger a}{\rho}_+\rp+n_\text{Th}\lp2a^\dagger\rho a-\comm{a\,a^\dagger}{\rho}_+\rp\rp\]](form_2.png)
 ,
, 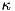 , and
, and 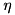 , representing the mode frequency, loss rate, and pumping Rabi frequency, respectively. A dimensionless parameter is
, representing the mode frequency, loss rate, and pumping Rabi frequency, respectively. A dimensionless parameter is 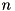 (the average number of thermal photons in the heat bath) and the cutoff of the Fock space.
(the average number of thermal photons in the heat bath) and the cutoff of the Fock space.![\[J_0=\sqrt{2\kappa(n_\text{Th}+1)}a,\quad J_1=\sqrt{2\kappa n_\text{Th}}a^\dagger.\]](form_6.png)
![\[\HnH=\lp-\delta-i\kappa(2n_\text{Th}+1)\rp a^\dagger a+\lp\eta a^\dagger+\hermConj\rp\equiv-iz\,a^\dagger a+\lp\eta a^\dagger+\hermConj\rp,\]](form_7.png)
![\[z\equiv\kappa(2n_\text{Th}+1)-i\delta.\]](form_8.png)
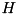 itself but
itself but 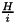 has to supplied!
has to supplied!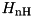 above. The ladder operator in interaction picture is
above. The ladder operator in interaction picture is ![\[a\Int(t)=a e^{-zt},\]](form_12.png)
![\[H\Int(t)=\lp\eta a^\dagger e^{zt}+\eta^*ae^{-zt}\rp.\]](form_13.png)
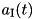 and
and 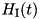 :
: ![\[H_\text{X-X}=g(a+a^\dagger)(b+b^\dagger).\]](form_16.png)
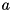 or
or 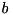 or both may be in interaction picture. Here, for the sake of simplicity, we assume that both constituents are of the type
or both may be in interaction picture. Here, for the sake of simplicity, we assume that both constituents are of the type ![\[H_{\text{X-X;I}}(t)=g(ae^{-z_at}+a^\dagger e^{z_at})(be^{-z_bt}+b^\dagger e^{z_bt}).\]](form_19.png)
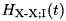 , which result from the use of interaction picture.
, which result from the use of interaction picture.
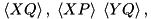 and
and 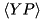 between the modes, where
between the modes, where 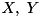 and
and 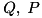 are the quadratures of the two modes, respectively. The element can be derived from the former interaction element in the inheritance-based design:
are the quadratures of the two modes, respectively. The element can be derived from the former interaction element in the inheritance-based design: 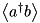 and
and 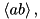 respectively.
respectively.