Table Of Contents
Previous topic
Iterator—Notes on implementation
Next topic
Quick search
Enter search terms or a module, class or function name.
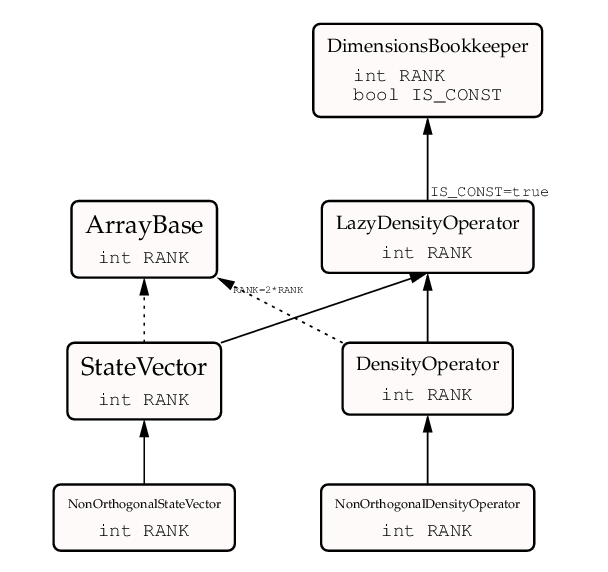
The quantumdata namespace comprises classes which represent the state of composite quantum systems and provide various interfaces to manipulate this data. Some of its most important classes fit into a single class hierarchy, which may be sketched as follows:
Template argument definitions
In a quantum-simulation framework, users should be able to write code for calculating quantum expectation values from quantumdata, independently of whether this data is represented by state vectors or density operators, in orthogonal or non-orthogonal bases. One obvious solution is relying on the formula
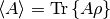
(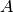 being an observable and
being an observable and 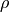 the density operator of the system), to write code only for the density-operator case, and fall back to this in the state-vector case as well, by calculating a dyad from the state vector. This is, however, extremely wasteful, since usually not all the matrix elements of
the density operator of the system), to write code only for the density-operator case, and fall back to this in the state-vector case as well, by calculating a dyad from the state vector. This is, however, extremely wasteful, since usually not all the matrix elements of 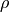 are needed for calculating the average, furthermore, for large dimensionality this solution may become outright unaffordable in terms of memory: for large systems, we may afford to store
are needed for calculating the average, furthermore, for large dimensionality this solution may become outright unaffordable in terms of memory: for large systems, we may afford to store 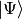 , but not
, but not 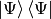 .
.
The solution adopted for this problem in the framework is represented by the class LazyDensityOperator, which provides a common interface for all the four cases StateVector, DensityOperator, and their non-orthogonal counterparts, to calculate quantum averages from their data. The “laziness” means that in the case of state vectors only those elements of the density operator are calculated that are actually asked for.
template <int RANK> (cf. template parameters); inherits publicly from DimensionsBookkeeper<RANK,true>
This class is totally inmutable, all its member functions being constant.
Inherited from DimensionsBookkeeper
The type used for indexing the “rows” and the “columns”, this is either an index, or a multi-index, in the latter case represented by a TTD_IdxTiny:
typedef typename mpl::if_c<(RANK==1),int,TTD_IdxTiny<RANK> >::type Idx;
// Idx is just an int if RANK==1, otherwise a TinyVector of ints
Constructor (protected)
The indexing function, purely virtual.
An inline function for conveniently addressing the diagonal elements:
double operator()(const Idx& i) const {return real((*this)(i,i));}
template <typename V> (cf. template parameters)
These functions return the quantumdata::ldo::DiagonalIterators corresponding to the start and end of the sequence of slices defined by V (cf. the section on slicing a LazyDensityOperator).
Semantics
Assume a mode represented in Fock basis with ladder-operator  . To calculate the quantum expectation value
. To calculate the quantum expectation value
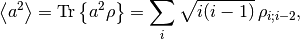
one can write the following function:
include "LazyDensityOperator.h"
const dcomp calculateASqr(const LazyDensityOperator<1>& matrix)
{
dcomp res;
for (int i=2; i<matrix.getTotalDimension(); ++i) res+=sqrt(i*(i-1))*matrix(i,i-2);
return res;
}
- Binary system
Assume two modes represented in Fock bases with ladder-operators
and
, respectively. To calculate the quantum expectation value
one can write the following function:
include "LazyDensityOperator.h" const dcomp calculateADaggerB(const LazyDensityOperator<2>& matrix) { typedef LazyDensityOperator<2>::Idx Idx; const LazyDensityOperator<2>::Dimensions dim(matrix.getDimensions()); dcomp res; for (int i=0; i<dim[0]-1; ++i) for (int j=1; j<dim[1]; ++j) res+=sqrt((i+1)*j)*matrix(Idx(i,j),Idx(i+1,j-1)); return res; }
We rely on the covariant-contravariant formalism to represent these in the framework.
The user has considerable freedom in how the metrical transformation for a given non-orthogonal basis is defined, the only requirement being that there is a specialized instant of quantumdata::transformation::Traits for the type representing the transformation. When compositing elementary Hilbert spaces, the framework takes care of the correct composition of the elementary metrical transformations. Of course, once there is a single non-orthogonal component, the whole composite has to be represented by non-orthogonal classes, in which case the system substitutes a quantumdata::transformation::Identity dummy transformation for the metrics of such components as are represented in orthogonal bases.
Note
The infrastructure for representing non-orthogonals is not yet fully matured, and will not be made fully available before Milestone 11.
Analogously to state vectors, it is also necessary to slice LazyDensityOperators because for calculating quantum expectation values of subsystem-observables (e.g. in Composites), the partial-trace density operator is needed. For the partial trace, however, only such elements of the full density operator are needed as are diagonal in the indeces not belonging to the given subsystem (dummy indeces). This is the reason why the tool performing the iteration is called DiagonalIterator.
Slicing is fully recursive, a sliced LazyDensityOperator (usually obtained by dereferencing a DiagonalIterator) can be further sliced.
On higher levels of the framework, the iteration is performed via the function:
template<typename V, typename T, int RANK, typename F> (cf. template parameters)
const T(const typename ldo::DiagonalIterator<RANK,V>::value_type&)
template<typename V, typename T, int RANK, typename F>
const T
partialTrace(const LazyDensityOperator<RANK>& matrix, F function)
{
ldo::DiagonalIterator<RANK,V> begin(matrix.template begin<V>());
T init(function(*begin));
using namespace cpputils;
return T(
accumulate(++begin,
matrix.template end<V>(),
init,
function,
cpputils::plus<T>()
)
);
}
Semantics
The function iterates through all the combinations of the dummy indeces, for each slice it takes the value returned by the functor function, and accumulates these values. In the following we give some instructive examples of usage.
Assume having a function which simply copies the content of a unary LazyDensityOperator into a structure::free::DensityOperatorLow:
using structure::free::DensityOperatorLow
const DensityOperatorLow
densityOperator(const LazyDensityOperator<1>& m)
{
size_t dim=m.getDimension();
DensityOperatorLow res(dim,dim);
for (int i=0; i<dim; i++) for (int j=0; j<dim; j++) res(i,j)=m(i,j);
return res;
}
Then the partial density operator of any unary subsystem of a system of any rank may be calculated as follows (e.g. from a StateVector):
template<int RANK, int SUBSYSTEM> // for the subsystem indexed by the index SUBSYSTEM
const DensityOperatorLow
partialTraceOfUnarySubsystem(const StateVector<RANK>& psi)
{
return partialTrace<tmptools::Vector<SUBSYSTEM>,DensityOperatorLow>(psi,densityOperator);
}
Assume having the function calculateADaggerB as defined above. Then, if these modes are embedded at index positions 3 and 1 (note that the order might be important) in a larger system of arity larger than 3, we can write the following function:
template<int RANK> // RANK>3
const dcomp
calculateADaggerB_atPositions3and1(const LazyDensityOperator<RANK>& matrix)
{
return partialTrace<tmptools::Vector<3,1>,dcomp>(matrix,calculateADaggerB);
}
This will calculate 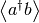 (now
(now 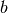 and
and  being the ladder operators of the modes at position 1 and 3, respectively) for the partial density operator of the embedded system (but without explicitly calculating this partial density operator).
being the ladder operators of the modes at position 1 and 3, respectively) for the partial density operator of the embedded system (but without explicitly calculating this partial density operator).
An arbitrary ensemble of real or complex numbers can be stored in a TTD_DArray<1> or TTD_CArray<1> (or even std::valarrays), as these types fulfill all the requirements on type T. The former was used to define the abstract interface structure::Averages, one implementation being Mode.
E.g. a function for a harmonic-oscillator mode calculating 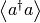 ,
, 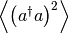 , and the real and imaginary parts of
, and the real and imaginary parts of 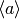 , may be defined as
, may be defined as
typedef TTD_DArray<1> Averages;
const Averages
calculateModeAverages(const LazyDensityOperator<1>& matrix)
{
Averages averages(4); averages=0;
for (int n=1; n<int(matrix.getDimension()); n++) {
double diag=matrix(n);
averages(0)+= n*diag;
averages(1)+=n*n*diag;
double sqrtn=sqrt(double(n));
dcomp offdiag(matrix(n,n-1));
averages(2)+=sqrtn*real(offdiag);
averages(3)+=sqrtn*imag(offdiag);
}
return averages;
}
Then the following function will calculate these averages for a mode embedded in a larger system at index position MODE_POSITION:
template<int RANK, int MODE_POSITION> // for the subsystem indexed by the index MODE_POSITION
const Averages
calculateEmbeddedModeAverages(const StateVector<RANK>& psi)
{
return partialTrace(psi,calculateModeAverages,tmptools::Vector<MODE_POSITION>(),Averages());
}
template<int RANK, typename V> (cf. template parameters)
Calculates the negativity of the partial transpose of the density operator of an arbitrarily complex system. Of course it should be regarded as a bipartite system, so that a subsystem has to be specified to be one party of the bipartite. The compile-time vector V specifies the subsystem.
The negativity is calculated as the sum of the negative eigenvalues of the partially transposed density operator.
Note
This definition is equivalent to the original definition of Vidal and Werner [1] up to a sign, because the partially transposed density operator’s eigenvalues come in two sorts:
- solitary positive numbers (
) adding up to one
- pairs of opposite-sign numbers (
)
Footnotes
| [1] |
|