Implementing a harmonic-oscillator mode¶

We demonstrate how to implement an element representing a pumped lossy mode in a truncated Fock space. In the frame rotating with the pump frequency, it is described by the Hamiltonian:

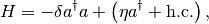
(1) $H=-\delta a^\dagger a+\lp\eta a^\dagger+\hermConj\rp,$

where $\delta$ is the detuning between the oscillator and the pump frequencies. The Liouvillean:

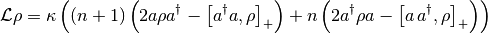
$\Liou\rho=\kappa\lp(n+1)\lp2a\rho a^\dagger-\comm{a^\dagger a}{\rho}_+\rp+n\lp2a^\dagger\rho a-\comm{a\,a^\dagger}{\rho}_+\rp\rp$

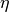The frequency-like parameters are $\delta$ , $\kappa$ , and $\eta$ , representing the mode frequency, loss rate, and pumping Rabi frequency, respectively. A dimensionless parameter is 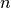$n$ (the average number of thermal photons in the heat bath) and the cutoff of the Fock space.

Using the notation of Sec. Description of the MCWF method,

$J_0=\sqrt{2\kappa(n+1)}a$

$J_1=\sqrt{2\kappa n}a^\dagger$

The non-Hermitian Hamiltonian for the Monte Carlo wave-function method reads:

(2) $\HnH=\lp-\delta-i\kappa(2n+1)\rp a^\dagger a+\lp\eta a^\dagger+\hermConj\rp\equiv-iz\,a^\dagger a+\lp\eta a^\dagger+\hermConj\rp$

where we have introduced the complex frequency

$z\equiv\kappa(2n+1)-i\delta$

The element has to be represented by a class which inherits publicly from the necessary classes in the structure namespace. In this simple case, it is basically two helper functions returning quantumoperator::Tridiagonals, a constructor, and two virtual functions inherited from ElementAveraged that have to be written. Consider the file ExampleMode.h [1]:

See also

The description of Tridiagonal

#include "Free.h"
#include "TridiagonalHamiltonian.h"
#include "ElementLiouvillean.h"
#include "ElementAveraged.h"

using namespace structure;
using namespace free;


const Tridiagonal aop(size_t);
const Tridiagonal nop(size_t);


class PumpedLossyMode 
  : public Free, public TridiagonalHamiltonian<1,false>, public ElementLiouvillean<1,2>, public ElementAveraged<1>
{
public:
  typedef ElementAveraged<1>::LazyDensityOperator LazyDensityOperator;

  PumpedLossyMode(double delta, double kappa, dcomp eta, double n, size_t cutoff);

private:
  const Averages average_v(const LazyDensityOperator&) const;
  void           process_v(Averages&)                  const {}

};

This will suffice here. Let us look at the implementations in ExampleMode.cc:

#include "ExampleMode.h"

#include <boost/assign/list_of.hpp>

#include <boost/bind.hpp>

using boost::assign::tuple_list_of; using boost::assign::list_of; using boost::bind;


void aJump   (StateVectorLow&, double kappa_nPlus1);
void aDagJump(StateVectorLow&, double kappa_n     );

double aJumpProba   (const LazyDensityOperator&, double kappa_nPlus1);
double aDagJumpProba(const LazyDensityOperator&, double kappa_n     );


PumpedLossyMode::PumpedLossyMode(double delta, double kappa, dcomp eta, double n, size_t cutoff)
  : Free(cutoff,
	 RealFreqs(),
	 tuple_list_of
	 ("(kappa*(2*n+1),delta)",dcomp(kappa*(2*n+1),delta),cutoff)
	 ("eta",eta,sqrt(cutoff))),
    TridiagonalHamiltonian<1,false>(dcomp(-kappa*(2*n+1),delta)*nop(cutoff)
                                    +
                                    tridiagPlusHC_overI(conj(eta)*aop(cutoff))),
    ElementLiouvillean<1,2>(JumpStrategies(bind(aJump   ,_1,kappa*(n+1)),
                                           bind(aDagJump,_1,kappa* n   )),
                            JumpProbabilityStrategies(bind(aJumpProba   ,_1,kappa*(n+1)),
                                                      bind(aDagJumpProba,_1,kappa* n   )),
			    "Mode",list_of("photon loss")("photon absorption")),
    ElementAveraged<1>("PumpedLossyMode",
                       list_of("<number operator>")("real(<ladder operator>)")("imag(\")"))
{
  getParsStream()<<"# Pumped lossy mode";
}


const PumpedLossyMode::Averages PumpedLossyMode::average_v(const LazyDensityOperator& matrix) const
{
  Averages averages(3);

  averages=0;

  averages(0)=aJumpProba(matrix,1);

  for (int n=1; n<int(matrix.getDimension()); n++) {
    double sqrtn=sqrt(n);
    dcomp offdiag(matrix(n,n-1));
    averages(1)+=sqrtn*real(offdiag);
    averages(2)+=sqrtn*imag(offdiag);
  }

  return averages;

}

Lines 18-22:

We construct the Free base with the dimension of the system and the tuples for the frequency-like parameters of the system, which in this case are all complex (cf. explanation). The tool from Boost.Assign facilitates the creation of lists of such tuples.

Lines 23-25:

We construct the time-independent TridiagonalHamiltonian base. This is greatly facilitated by the algebra and helpers of the quantumoperator::Tridiagonal class.

Warning

When implementing the Hamiltonian, not 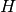$H$ itself but 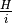$\frac Hi$ has to supplied!

Lines 26-30:

We construct the ElementLiouvillean base whose second template argument denotes the number of different quantum jumps, which is 2 in this case. The constructor takes the strategies for calculating the impact of a jump on a StateVectorLow, and for calculating the probability from a LazyDensityOperator. These strategy functions are produced from the free-standing helpers in Lines 10-14 through binding.

Lines 31-32:

We construct the ElementAveraged base, with parameters necessary to produce a simple key for quantum averages communicated towards the user. Here we calculate only three such averages, the expectation value of the number operator, and the real and imaginary parts of that of the ladder operator.

Lines 38-55:

The inherited function average() is implemented.

Line 44:: the expectation value of the photon number is calculated (where we can reuse our function aJumpProba, with unit loss rate).
Lines 49-50:: the expectation value of the ladder operator is calculated

The implementation of the helpers is also quite straightforward. It may come to a separate file ExampleModeImpl.cc:

#include "ExampleMode.h"


void aJump   (StateVectorLow& psi, double kappa_nPlus1)
{
  double fact=sqrt(2.*kappa_nPlus1);
  int ubound=psi.ubound(0);
  for (int n=0; n<ubound; ++n)
    psi(n)=fact*sqrt(n+1)*psi(n+1);
  psi(ubound)=0;
}


void aDagJump(StateVectorLow& psi, double kappa_n     )
{
  double fact=sqrt(2.*kappa_n);
  for (int n=psi.ubound(0); n>0; --n)
    psi(n)=fact*sqrt(n)*psi(n-1);
  psi(0)=0;
}


double photonNumber(const LazyDensityOperator& matrix)
{
  double res=0;
  for (size_t n=1; n<matrix.getDimension(); ++n)
    res+=n*matrix(n);
  return res;
}


double aJumpProba   (const LazyDensityOperator& matrix, double kappa_nPlus1)
{
  return 2.*kappa_nPlus1*photonNumber(matrix);
}


double aDagJumpProba(const LazyDensityOperator& matrix, double kappa_n     )
{
  return 2.*kappa_n*(photonNumber(matrix)+1.);
}


const Tridiagonal::Diagonal mainDiagonal(const dcomp& z, size_t dim)
{
  Tridiagonal::Diagonal res(dim);
  res=blitz::tensor::i;
  return res*=z;
}


const Tridiagonal aop(size_t dim)
{
  typedef Tridiagonal::Diagonal Diagonal;
  Diagonal diagonal(dim-1);
  return Tridiagonal(Diagonal(),1,Diagonal(),diagonal=sqrt(blitz::tensor::i+1.));
}


const Tridiagonal nop(size_t dim)
{
  return Tridiagonal(mainDiagonal(1.,dim));
}

Warning

In situations like the one in Line 56, it is extremely important to write blitz::tensor::i+1., otherwise the blitz::sqrt function will operate within the integers, which is perhaps a shortcoming of the Blitz++ library in this respect.

Interaction picture¶

In many situations, it pays to transfer to interaction picture defined by the first term of the Hamiltonian (1). The ladder operator in interaction picture is

(3) $a\Int(t)=a e^{-zt},$

so that the Hamiltonian reads

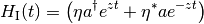
(4) $H\Int(t)=\lp\eta a^\dagger e^{zt}+\eta^*ae^{-zt}\rp$

See also

These notes about how to treat interaction pictures defined by non-unitary transition operators in a consistent way.

In this case, the class representing the element has to be derived from Exact as well, which represents the transformation between the two pictures. In addition, instead of TridiagonalHamiltonian<1,false>, we need to derive from TridiagonalHamiltonian<1,true>, because the Hamiltonian is now time-dependent.

Note

In general usage, the jump and the averages are calculated in the normal picture also in this case (cf. explanation of classes structure::Hamiltonian, structure::Exact, structure::Liouvillean, and structure::Averaged, and furthermore Sec. MCWF trajectory). This allows for reusing the same code in both pictures. (Incidentally, here the Liouvillean remains unchanged anyway.)

#include "Free.h"
#include "TridiagonalHamiltonian.h"
#include "ElementLiouvillean.h"
#include "ElementAveraged.h"
#include "FreeExact.h"

using namespace structure;
using namespace free;



class PumpedLossyModeIP
  : public Free, public FreeExact, public TridiagonalHamiltonian<1,true>, public ElementLiouvillean<1,2>, public ElementAveraged<1>
{
public:
  typedef ElementAveraged<1>::LazyDensityOperator LazyDensityOperator;

  PumpedLossyModeIP(double delta, double kappa, dcomp eta, double n, size_t cutoff);

  const dcomp get_z() const {return z_;}

private:
  void updateU(double dtDid) const;

  bool isUnitary_v() const {return true;}

  const Averages average_v(const LazyDensityOperator&) const;
  void           process_v(Averages&)                  const {}

  const dcomp z_; // Needed for updateU

};


const Tridiagonal aop(const PumpedLossyModeIP&);

In the implementation, the only difference from the previous case will be the constructor, because the Hamiltonian now also requires furnishing with frequencies, and the implementation of the virtual function updateU().

When “furnished with frequencies”, a quantumoperator::Tridiagonal object will internally take care about the time-dependent phases appearing in (3) and (4).

const Tridiagonal::Diagonal mainDiagonal(const dcomp& z, size_t cutoff);


PumpedLossyModeIP::PumpedLossyModeIP(double delta, double kappa, dcomp eta, double n, size_t cutoff)
  : Free(cutoff,
	 tuple_list_of
	 ("kappa*(2*n+1)",kappa*(2*n+1),cutoff)
	 ("delta",delta,1),
	 tuple_list_of
	 ("eta",eta,sqrt(cutoff))),
    FreeExact(cutoff),
    TridiagonalHamiltonian<1,true>(furnishWithFreqs(tridiagPlusHC_overI(conj(eta)*aop(cutoff)),
                                                    mainDiagonal(dcomp(kappa*(2*n+1),-delta),cutoff))),
    ElementLiouvillean<1,2>(JumpStrategies(bind(aJump   ,_1,kappa*(n+1)),
                                           bind(aDagJump,_1,kappa* n   )),
                            JumpProbabilityStrategies(bind(aJumpProba   ,_1,kappa*(n+1)),
                                                      bind(aDagJumpProba,_1,kappa* n   )),
                            "Mode",list_of("photon loss")("photon absorption")),
    ElementAveraged<1>("PumpedLossyMode",
                       list_of("<number operator>")("real(<ladder operator>)")("imag(\")")),
    z_(kappa*(2*n+1),-delta)
{}


void PumpedLossyModeIP::updateU(double dtDid) const
{
  getFactors()=exp(-z_*(dtDid*blitz::tensor::i));
}

FreeExact assumes that the operator transforming between the two pictures is diagonal, and the factors to update are simply its diagonal elements. If this is not the case, Exact has to be used instead.

The construction of the object representing the ladder operator furnished with frequencies is also straightforward:

const Tridiagonal aop(const PumpedLossyModeIP& mode)
{
  size_t dim=mode.getDimension();
  return furnishWithFreqs(aop(dim),mainDiagonal(mode.get_z(),dim));
}

Note

Since a lot of the code from the previous case can be reused here, one will usually adopt an inheritence- or class-composition-based solution to implement classes like PumpedLossyMode and PumpedLossyModeIP (cf. Mode).

Implementing an X-X interaction¶

Let us consider the interaction described by the Hamiltonian

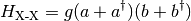
$H_\text{X-X}=g(a+a^\dagger)(b+b^\dagger)$

The class implementing this interaction has to be derived from Interaction<2> because it is a binary interaction, and TridiagonalHamiltonian<2,...> (note that quantumoperator::Tridiagonal is capable to represent direct products of tridiagonal matrices).

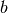The only thing requiring some care is that once we transform some elements into interaction picture, the whole Hamiltonian is transformed, that is, $a$ or $b$ or both may be in interaction picture. Here, for the sake of simplicity, we assume that both constituents are of the type PumpedLossyModeIP. Hence, the Hamiltonian is in fact

(5) $H_{\text{X-X;I}}(t)=g(ae^{-z_at}+a^\dagger e^{z_at})(be^{-z_bt}+b^\dagger e^{z_bt}).$

Consider ExampleInteraction.h:

#include "ExampleMode.h"
#include "Interaction.h"


class InteractionX_X
  : public Interaction<2>, public TridiagonalHamiltonian<2,true>
{
public:
  InteractionX_X(const PumpedLossyModeIP&, const PumpedLossyModeIP&, double g);

};

ExampleInteraction.cc then reads

#include "ExampleInteraction.h"

#include "SmartPtr.h"
using cpputils::sharedPointerize;

#include <boost/assign/list_of.hpp>
using boost::assign::tuple_list_of;

InteractionX_X::InteractionX_X(const PumpedLossyModeIP& m0, const PumpedLossyModeIP& m1, double g)
  : Interaction<2>(Frees(sharedPointerize(m0),sharedPointerize(m1)),tuple_list_of("g",g,sqrt(m0.getDimension()*m1.getDimension()))),
    TridiagonalHamiltonian<2,true>(g*
				   (aop(m0)+aop(m0).dagger())*
				   (aop(m1)+aop(m1).dagger())
				   )
{}

As we see, the Hamiltonian can be written in a rather straightforward way, and it internally takes care about the time-dependent phases appearing in (5), which result from the use of interaction picture.

Footnotes

[1]	The files referred to in this Section are found in directory `doc/examples` in the distribution. The code examples are expected to compile, cf. `doc/examples/Jamfile`.

Table Of Contents

Previous topic

Next topic

Implementing a harmonic-oscillator mode¶

Interaction picture¶

Implementing an X-X interaction¶

Navigation

Table Of Contents

Previous topic

Next topic

Quick search

Implementing a harmonic-oscillator mode¶

Interaction picture¶

Implementing an X-X interaction¶

Navigation