Table Of Contents
- C++QEDv2 User Guide
Previous topic
C++QED: a framework for simulating open quantum dynamics
Next topic
Quick search
Enter search terms or a module, class or function name.
This guide is meant to allow for understanding and using the framework on the highest level, that is, for building simulations out of the already existing modules and elementary systems as building blocks.
C++QED is a framework for simulating open quantum dynamics in general. Originally it was developed for problems in moving-particle cavity QED, but subsequently has been applied in other fields as well. It has demonstrated the ability to simulate full Master equation of up to several thousand, and quantum trajectories of up to several hundred thousand dimensions.
The framework’s basic idea is to allow users to build arbitrarily complex interacting quantum systems from elementary free subsystems and interactions (below these are commonly referred to as elements), and simulate their time evolution with a number of available time-evolution drivers. Operating with elementary physical systems, the interface is of a much higher level than that in the popular Quantum Optics Toolbox for Matlab [Matlab], or the much less known, but venerable QSD (Quantum State Diffusion) C++ library [QSD]. In both, the interface is built on quantum operators, and general usage involves a considerable amount of boilerplate.
C++QEDv2 specifies a small grammar to describe composite quantum systems. Apart from providing a number of elements out of the box, there are several tools which facilitate the implementation of new elements. These are being added continuously, as the need arises.
The framework saw a first release (v1), which was also partially documented in a journal article [EPJD]. As to physics, this paper still applies, and the reader should consult it if something is not clear from the physics point of view in the following. The differences between C++QEDv1 and v2 are so numerous that it is easier to describe the similarities, which essentially lie in the basic idea of the interface as described above. Because of this, and despite all the differences, experience has shown that it is not difficult migrate elements and scripts written for v1 to v2. C++QEDv1 relied on a pure object-oriented design, while in v2 the emphasis is more on generic programming and TMP. In particular, the principal concept of the design of C++QEDv2 is that all information available at compile time should be processed as such, with the help of TMP. All in all, v1 can be regarded as a prototype of v2.
At the moment the following possibilities for time evolution are provided in the framework (cf. The quantumtrajectory namespace):
A number of other methods, e.g. the quantum state diffusion, can be easily incorporated into the framework.
Note
In the case when the probability of quantum jumps vanishes, the MCWF method reduces to the simulation of the Schrödinger equation, so the latter is naturally – and without overhead – available in the framework.
The framework is very sensitive to performance both in terms of computer resources and coding/design. In the latter aspect the goal, as always in software architecture, is to create maximally reusable code. Perhaps the most spectacular example is that the very same code, if it is written generally enough, can be used to calculate MCWF and full Master-equation evolution.
In the former aspect, there are physical and computational methods to increase performance. Among the physical ones, the most notable is the maximal use of interaction picture, which may help to get rid of very separate timescales in the problem. Among the computational ones we can mention
In addition, we have to note that simulation of moving particles is inherently hard, since the Schrödinger equation is a partial differential equation, and we inevitably have to deal with both position and momentum representations, which are linked by Fourier transformation. In our problems, however, the particles are mostly moving in potentials created by electromagnetic fields, mainly standing and running waves. In this case we can stay in momentum space during the whole time evolution, and no FFT is necessary (cf. [EPJD] and Particle in momentum space).
A strange consequence is that in numerical physics the harmonic oscillator seems to be hard, while the cosine potential is easy.
Binary packages have been prepared for Ubuntu which might also work on Debian (not tested). Installation from binary packages is recommended for users who want to try C++QED or use it exclusively on its highest level, i.e. writing scripts which use elements and interactions already implemented in C++QED. If you are not using Ubuntu or want to develop your own elements and interactions you have to install C++QED from source.
To install the binary packages
% sudo add-apt-repository ppa:raimar-sandner/cppqed
% sudo apt-get update
% sudo apt-get install libc++qed-dev c++qed-scripts
This will install all necessary dependencies and the following three packages:
If you want to start developing your own scripts, copy the example project directory /usr/share/doc/libc++qed-<version>-dev/examples to some place convenient and refer to the file Readme.txt in this directory for instructions.
In the following we will cover how to use the framework on the highest level. The highest level is a C++ program, which is called a script. A Python frontend is currently under development, and a GUI might eventually be provided, too.
A script creates an executable which defines and simulates a system of a particular layout. All information pertaining to the layout of the system is processed at compile time. Our compile-time algorithms can be regarded as C++ programs generating C++ programs in such a way that in the resulting executable all the compile-time information is encoded to yield a maximally efficient executable for the given layout.
A script is composed of a part where the system is specified, and another, where we do something with the system, most notably simulate its time evolution in one of the ways described in the Synopsis.
The simplest case is when we want to simulate a free system alone. Assume that this free system is a mode of a cavity (cf. Mode), which can be pumped and is lossy. We begin with defining the system, which is trivial in this case:
PumpedLossyMode mode(delta,kappa,eta,cutoff);
Once we have defined a system, we can already use it for several things, e.g. to calculate the action of the system Hamiltonian on a given state vector, but since C++QED is a “framework for simulating open quantum dynamics”, we will probably want to do something more.
Suppose we want to run a single MCWF trajectory. The system is started from a pure initial state, which may be specified as
quantumdata::StateVector<1> psi(mode::coherent(alpha,cutoff));
that is, the mode is in a coherent state with amplitude alpha (cf. mode::coherent()). StateVector<1> means that it is a state vector of a system featuring a single quantum number.
Next, we define our MCWF_Trajectory<1>:
quantumtrajectory::MCWF_Trajectory<1> trajectory(psi,mode,...a lot more parameters...);
The first two parameters are clear, the only thing to note is that psi is taken as a reference here, so the initial psi will be actually evolved as we evolve the trajectory. A lot more parameters are needed, pertaining to the ODE stepper, the random number generation, etc., but, as we will see below, the user will usually not have to worry about these.
All that remains is to run the trajectory, which is accomplished by
runDt(trajectory,time,dt);
This will evolve trajectory for time time, and display information about the state of the system after every time interval dt. What information is displayed is defined by the system. There is another version, which can be invoked like this:
run(trajectory,time,dc);
Here, dc is expected to be an integer, and it is the number of (adaptive) timesteps between two displays. This version is actually more suited to the physics of the problem, since the timesteps will be small, when many things are happening, and this is when we want more output, too. Cf. runDt(), run().
In the above, the necessary parameters must be previously defined somewhere. Parameters can of course come from several sources, but the most useful alternative is to have sensible defaults for all parameters, and to be able to override each of them separately in the command line when the program is actually executed with a given set of parameters. This allows for a very fine-grained control over what is to be accepted as default and what is to be overridden, and the command line never gets crowded by those parameters for which the default is fine.
This possibility is indeed supported by the framework, cf. Pars. Consider the following program [1]:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 | #include "Evolution.h"
#include "Mode.h"
int main(int argc, char* argv[])
{
ParameterTable p;
ParsEvolution pe(p); // Driver parameters
mode::ParsPumpedLossy pm(p); // Mode parameters
pe.evol=EM_MASTER;
pm.cutoff=30;
// ... other default values may follow
update(p,argc,argv,"--"); // Parsing the command line
// ****** ****** ****** ****** ****** ******
mode::Ptr mode(make(pm,QMP_UIP));
mode::StateVector psi(init(pm));
evolve(psi,mode,pe);
}
|
This is a full-fledged script, so if you copy this into directory scripts under the name of temp.cc, it will compile. Don’t forget to re-run cmake in order to pick up the new script and call
make temp
in the build directory. Alternatively, if you use bjam, compile the script with
bjam [release] temp
Let us analyse the script line by line:
ParameterTable is the module from our utility library utils which stores all the parameters of the problem, and enables them to be manipulated from the command line. It can store any type for which i/o operations are defined.
We instantiate the actual parameters for the time-evolution driver(s) and the mode, respectively. All the modules in the framework provide corresponding Pars... classes.
We specify the desired default values, e.g. we set that the default evolution mode should be Master equation [2].
The command line is parsed by the update() function. Parsing is not very sophisticated at the moment, but some errors do get detected at this point.
In the next line, we instantiate our mode, but now instead of the concrete PumpedLossyMode class, we are using a make (or dispatcher) function, which selects the best mode class corresponding to the parameters. There are 10 possibilities:
|
|
|
|
|
Roughly speaking, mode::Ptr is an entity that can store either of these classes. E.g. if kappa=0, and eta=0, then we will have a Mode; if eta is nonzero, a PumpedMode; and if both are nonzero, a PumpedLossyMode. The significance of this is that e.g. if the mode is not lossy, then the possibility of a quantum jump will not even be considered during time evolution, which speeds things up.
Sch, UIP and no suffix mean Schrödinger picture, unitary interaction picture, and “full” interaction picture, respectively. It is easy to see that if the system is not lossy, then the latter two coincide. Schrödinger picture is provided mostly for testing purposes, the performance is usually not optimal in this case.
See also
On the various degrees of interaction picture Interaction picture, Exploiting interaction picture
What we are telling the maker function in the same line is that the picture should be unitary interaction picture. Alternatively, we could add this as a parameter as well, which can be achieved by putting the line
QM_Picture& qmp=p.add("picture","Quantum mechanical picture",QMP_UIP);
anywhere between ParameterTable and update.
In the next line, mode::StateVector is just another name for quantumdata::StateVector<1>, and init() is just another dispatcher, this time for the initial condition of the mode.
Finally, in the last line evolve() is a dispatcher for different evolution modes and the two versions run() and runDt(). So with this, the evolution mode can be changed from the command line, e.g. depending on the dimension of the problem – while for low dimension we may use Master equation, for larger dimension we may need to switch to an ensemble of quantum trajectories. The possibilities are:
If we specify the --help option in the command line, the program will display all the available parameters together with their types (the less readable the more complex the type is), a short description, and the default value.
An example command line then looks like:
CppQedScript --eps 1e-12 --dc 100 --deltaC -10 --cutoff 20 --eta "(2,-1)" ...
There are some parameters that are “stronger” than others. E.g. if --dc is nonzero, then always the run() version will be selected by the evolve() function above, regardless of the value of --Dt. The latter will only be considered if --dc is zero because in this case the runDt() version will be selected. There is a similar relationship between --minitFock and --minit: the former will always override the latter.
Note
If --evol ensemble is selected, then always the runDt() version will be used. This is because when the averaging of the trajectories happens, all the trajectories must have reached exactly the same point in time.
Imagine we would like to define a more complex system, where a two-level atom (qbit) interacts with a single cavity mode with a Jaynes-Cummings type interaction. Both the qbit and the mode may be pumped, and they may also be lossy. First, we have to define the free elements of the system:
PumpedLossyQbit qbit(deltaA,gamma,etaA);
PumpedLossyMode mode(deltaC,kappa,etaC,cutoff);
or
qbit::ParsPumpedLossy pq(p);
mode::ParsPumpedLossy pm(p);
// ... update and whatever here
qbit::Ptr qbit(make(pq,QMP_IP));
mode::Ptr mode(make(pm,QMP_IP));
Here qbit::make() will dispatch exactly the same possibilities that we have seen for the mode above.
Next, we define the interaction between them:
JaynesCummings<> act(qbit,mode,g);
or
jaynescummings::Pars pjc(p);
// ... followed by
JaynesCummings<> act(qbit,mode,pjc);
Note
JaynesCummings is designed in such a way that it accepts not only concrete classes, but, loosely speaking, anything that qbit::Ptr and mode::Ptr can store. The same is true for all the interaction elements in the framework.
Now we have to bind together the two free subsystems with the interaction, which is simply accomplished by:
binary::Ptr system(binary::make(act));
In the case of a BinarySystem the complete layout of the system can be figured out from the single interaction element – and this is trivial. Similarly to mode::Ptr, binary::Ptr is an entity which can store all the versions of BinarySystem (for example, conservative or lossy).
BinarySystem is an extremely powerful module, whose design reflects the basic idea behind the framework. It internally handles all the loops and slicing that are necessary to calculate e.g. the effect of the Hamiltonian of the qbit component if it is part of a binary system. It acts and feels like any other system, like e.g., Qbit itself, the difference being that the latter has only one quantum number, while BinarySystem has two. A basic design principle of the framework is that it is fully recursive, that is, any composite system can act as an element of an even more complex system. [3]
Our next task is to define the initial condition:
StateVector<2> psi(qbit::state0()*mode::coherent(alpha,cutoff));
This is to say that the qbit is in its 0 state, and the mode is in a coherent state with amplitude alpha. Both states are of type StateVector<1>, meaning that they are state vectors featuring a single quantum number, and * means direct product of state vectors, so the result here is a StateVector<2>. Direct product is not commutative in this case, and we have to comply with the order defined above for the free systems. Alternatively, we could have said
StateVector<2> psi(init(pq)*init(pm));
From this point on, usage is the same as we have seen above for the mode example. Since in this case the system is a BinarySystem, it will reach into its constituents for the informations to display, supplying either with the corresponding reduced density operator (cf. LazyDensityOperator and its slicing), which contains all information on the state of the subsystem.
If the system is not to be used for anything else, just for being evolved, we can avoid having to invent all these redundant names like qbit, mode, act, system, trajectory, and create everything in place. In this case a full-fledged script can be as terse as:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 | #include "EvolutionBinary.h"
#include "JaynesCummings.h"
int main(int argc, char* argv[])
{
ParameterTable p;
ParsEvolution pe(p);
qbit::ParsPumpedLossy pq(p);
mode::ParsPumpedLossy pm(p);
jaynescummings::Pars pjc(p);
update(p,argc,argv,"--"); // Parsing the command line
quantumdata::StateVector<2> psi(init(pq)*init(pm));
evolve(psi,
binary::make(JaynesCummings<>(make(pq,QMP_IP),
make(pm,QMP_IP),
pjc)),
pe);
}
|
Each trajectory output has a header part, summarizing the parameters of the given simulation. The header displays system characteristics, and lists the decay channels of the system, each decay channel endowed with an ordinal number. This list facilitates the interpretation of log output.
Following the header part, the time-dependent simulated data is displayed, organized into columns. The first two columns are time and timestep, respectively, and then, separated by tab characters, the data stemming from the different subsystems follows. A key to the data (a short description of each column) is provided at the end of the header part.
In the case of a single MCWF trajectory, there is the option --logLevel, which, when nonzero, makes that the stepper will record certain data during the execution:
Reporting the number of failed ODE steps in the given step of the trajectory evolution.
See also
The discussion at MCWF trajectory and An adaptive MCWF method.
The output of real numbers has a precision of three digits by default, this can be overridden by the --precision option. This characteristic propagates throughout the framework from trajectory headers to state-vector outputs as follows:
- Trajectory header: real-number parameters of overall precision, but at least 6
- Time and timestep: of overall precision, but at least 6
- Quantum averages: of overall precision
- State-vector display within trajectories: of --svdPrecision whose default value 0 signifies falling back to the overall precision
- In .sv file:
- state-vector of overall precision
- time and timestep: of overall precision, but at least 6
Note
Parameters written by elements on paramsStream inherit the overall precision via a static data member of FormDouble.
The output can be piped into a file, or an output file specified with the --o option. For a single MCWF trajectory, in the latter case where the simulation comes to an end, the final state vector and the final state of the random-number generator will be stored in a corresponding file with extension .sv. This allows the framework to resume a trajectory, or the resulting state-vector can be reused as an initial condition for other trajectories.
If the file specified by the --o option already exist then the framework assumes that the trajectory has to be resumed from the final instant stored in the file. In this case a corresponding .sv file must also exist, which will be considered the state vector and the random-number-generator state at the final instant.
Note that a reasonable precision of the final-state output is crucial for correct continuation (cf. also this tracker)
A custom initial condition can be provided in a file whose name is passed to the framework by the --initFile option. If this option is given, it will override any other initial condition specified in the script.
If the framework has been compiled with Boost.Serialization dependence, it is possible to choose binary output for the final-state output (with extension .svbin in this case). This can be toggled with the --binarySVFile switch. This pertains also to trajectory continuation and initial-condition processing.
Note
If there are more than two free subsystems, the system can be much more complex. The number of possible interactions rises combinatorically with the number of frees. This is the situation when the full potential of C++QED is displayed.
For the description of the elements appearing in the following examples cf. Ref. [EPJD].
Assume we want to define a system where a particle is moving along the axis of a ring cavity, and is interacting with two counterpropagating running-wave modes of the cavity. Both of the modes are lossy, and one of them is pumped; the particle is not pumped. This system consists of three subsystems, a particle, and the two modes. There are three interactions:
We can lay out the system as the following simple network:

The Composite module of the framework is designed to represent such a network. Assume the following definitions are in effect:
// Instantiate Frees
Particle part (...);
LossyMode plus (...);
PumpedLossyMode minus(...);
// Instantiate Interactions
ParticleAlongCavity actP(plus ,part,...,MFT_PLUS );
ParticleAlongCavity actM(minus,part,...,MFT_MINUS);
ParticleTwoModes act3(plus,minus,part,...);
Here MFT_ means the type of the mode function and can be PLUS, MINUS, COS, and SIN [EPJD].
Then the system can be created by invoking the maker function for Composite with a helper class called Act:
composite::make(
Act<1,0> (actP),
Act<2,0> (actM),
Act<1,2,0>(act3)
);
What we are expressing here e.g. with the specification Act<1,2,0>(act3) is that the 0th “leg” of the interaction element ParticleTwoModes, which is the mode plus, is the 1st in our row of frees in the network above.
Note
Following C/C++ convention, all ordinals begin with 0 in the framework.
The 1st leg, the mode minus is the 2nd in the row; and the 2nd leg, the particle is the 0th in the row of frees. The legs of interaction elements cannot be interchanged, and we also have to be consistent with our preconceived order of frees throughout. Clearly, the three Act objects above contain all the information needed by the framework to figure out the full layout of the system.
Any inconsistency in the layout will result in a compile-time or runtime error. The user is encouraged to play around creating layout errors deliberately, and see what effect they have. Creating deliberate compilation errors as a response to misuse on a higher level, in such a way that the compiler is in addition forced to emit a sensible error message, is difficult. However, it is of course indispensable in template metaprogramming, if we want to leave any chance for ourselves to debug our metaprograms if something goes wrong. Here we are again relying on the Boost.MPL library.
The actual C++ type of a Composite object returned by such an invocation of composite::make() is quite complex, but a maker metafunction facilitates referencing it
composite::result_of::Make<Act<1,0>,Act<2,0>,Act<1,2,0> >::type
which is equivalent to:
Composite<composite::result_of::make_list<Act<1,0>,Act<2,0>,Act<1,2,0> >::type>
A full-fledged script in the terse way may read as:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 | #include "EvolutionComposite.h"
#include "ParticleTwoModes.h"
int main(int argc, char* argv[])
{
ParameterTable p;
ParsEvolution pe(p);
particle::Pars pp(p);
mode::ParsLossy pmP(p,"P");
mode::ParsPumpedLossy pmM(p,"M");
particlecavity::ParsAlong ppcP(p,"P");
particlecavity::ParsAlong ppcM(p,"M");
ppcP.modeCav=MFT_PLUS; ppcM.modeCav=MFT_MINUS;
update(p,argc,argv,"--");
particle::Ptr part (make(pp ,QMP_IP));
mode ::Ptr plus (make(pmP,QMP_IP));
mode ::Ptr minus(make(pmM,QMP_IP));
quantumdata::StateVector<3> psi(wavePacket(pp)*init(pmP)*init(pmM));
evolve(psi,
composite::make(
Act<1,0> (ParticleAlongCavity(plus ,part,ppcP)),
Act<2,0> (ParticleAlongCavity(minus,part,ppcM)),
Act<1,2,0>(ParticleTwoModes(plus,minus,part,ppcP,ppcM))
),
pe);
}
|
A notable additional feature as compared to previous examples is that since now we have two modes in the system, we somehow have to differentiate between their parameters in the command line. This is achieved by the "P" and "M" modifiers added to the constructors of Pars... objects, so that e.g. instead of --cutoff we now have the separate options --cutoffP and --cutoffM.
Although now all the frees have the general types contained by the mode::Ptr classes, their possible types are still restricted by the Pars... classes, such that e.g. plus can never become pumped.
Most of the interactions in C++QED will be binary, here we have seen an example for a ternary interaction. So far, we have encountered only a single example for a quaternary interaction.
Finally, we are reviewing one more example, which displays a last feature, which, in turn, reflects a basic principle of quantum physics: if two systems are identical, they are indistinguishable. In the language of C++QED this means that a single object is enough to represent them.
Consider two identical pumped particles moving in a direction orthogonal to the axis of a cavity sustaining a single lossy mode. The layout of the system is:
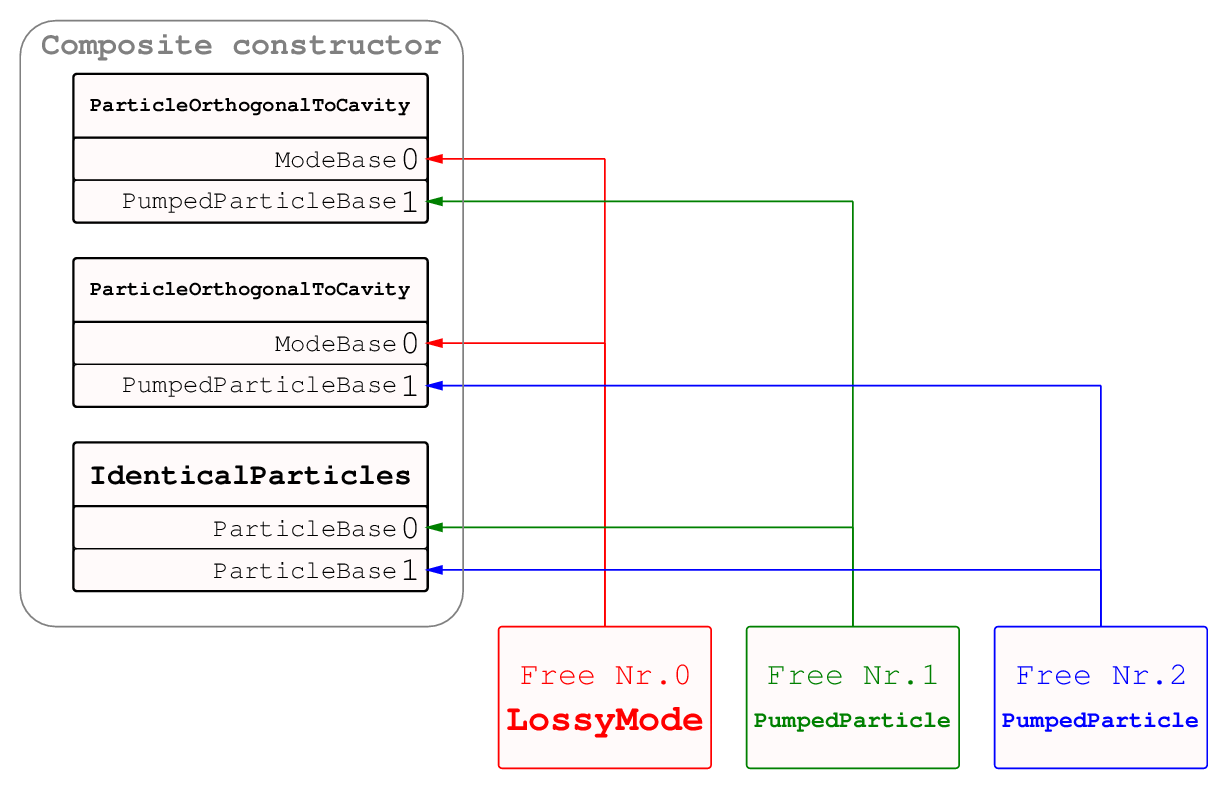
Without much ado we are quoting the kernel of a corresponding script:
1 2 3 4 5 6 7 8 9 10 11 12 13 | LossyMode mode(pm); // Free0
PumpedParticle part(pp); // Free1,2 - only one instant
ParticleOrthogonalToCavity act(mode,part,ppc); // only one instant
quantumdata::StateVector<3> psi(init(pm)*coherent(pp)*coherent(pp));
evolve(psi,
composite::make(
Act<0,1>(act),Act<0,2>(act),
Act<1,2>(IdenticalParticles<2>(part,...))
),
pe);
|
(A pumped particle can also be in a coherent state: a coherent state of the pump potential approximated as harmonic.)
In a composite system we may want to assess the entanglement between two parts of the system. This can be done using the negativity of the density operator’s partial transpose. Of course, since the dependence of this quantity on the density operator is not linear, this makes sense only in the case of Master-equation evolution or an ensemble of quantum trajectories. In the case we wish to assess the entanglement for a single trajectory, this can be achieved by choosing ensemble evolution and setting the number of trajectories to 1.
The subsystem to be considered as one party of the two has to be specified in an additional compile-time vector argument to the evolve() function.
See also
The discussion of quantumdata::negPT().
To show the syntax we assume e.g. that in the previous example we are looking for the entanglement between the two particles together as one party, and the mode as the other party. Then the invocation of evolve() is modified as
evolve<tmptools::Vector<1,2> >(psi,system,pe);
We simply have to list in the compile-time vector tmptools::Vector the frees that consist one party. Of course in this case this is equivalent to tmptools::Vector<0>.
The negativity will appear as a last column in the output, separated by a tab character from the rest.
For fast and easy interpretation, analysis and visualization of the data produced by C++QED there exists a Python library called PyCppQED. It also provides functions for creating convenient initial state vectors to be passed on to C++QED. With the help of this library, it is easy to write Python scripts for automated data processing.
The current release of the framework is C++QEDv2 Milestone 9, and it is a release corresponding to a new significant step in the documentation and to a paper in Computer Physics Communications [CPC]. The development is now in beta stage with no known major bugs. The foreseeable steps in the development are as follows:
PyCppQED is developed on github but releases will also be posted on the SourceForge project homepage of C++QED.
We offer full support for the framework both in terms of writing and testing new elements and scripts on demand from the quantum optics community, and of advising with the use of the existing software in the framework or with the development of new software (elements, scripts, time-evolution drivers). In the first case we may require to become co-author in the publications stemming from the work. In the second case we will probably only ask to please cite the journal articles on C++QED ([EPJD], [CPC]). We ask the same from anybody using C++QED without my support.
First of all, we would like to acknowledge the developers of Boost for making C++ an even more powerful language than it originally was. Without the Boost libraries, the framework could not have been achieved by a single person.
We would like to thank the developers of GSL, LAPACK, Blitz++, and FLENS for their effort, without which scientific computing in C++ in general, and the present framework in particular would not look as nice as it looks today.
| [Matlab] | S. M. Tan, A computational toolbox for quantum and atomic optics, J. Opt. B, 1, 424, (1999) |
| [QSD] | R. Schack and T. A. Brun, A C++ library using quantum trajectories to solve quantum master equations, Comp. Phys. Commun., 102, 210, (1997) |
| [EPJD] | (1, 2, 3, 4, 5) A. Vukics and H. Ritsch, C++QED: an object-oriented framework for wave-function simulations of cavity QED systems, Eur. Phys. J. D, 44, 585, (2007) |
| [CPC] | (1, 2) A. Vukics, C++QEDv2: The multi-array concept and compile-time algorithms in the definition of composite quantum systems, Comp. Phys. Commun., 183, 1381, (2012) |
Glossary
Some common command-line options of scripts
display the list of options
version information about the framework and underlying libraries
simulated time
ODE stepper relative and absolute precision
output frequency in number of ODE steps and in time, respectively
number of digits in the output of doubles throughout the framework
switching header output on (default) and off
random number generator seed
switching noise on (default) and off
number of trajectories for ensemble averaging
total jump probability limit
jump probability overshoot tolerance factor
switching negativity calculation on and off (default)
Footnotes
| [1] | Some of the code examples presented in this Guide can be found in the files doc/examples/tutorial[...].cc in the distribution. These files are expected to compile, cf. doc/examples/Jamfile. |
| [2] | Ultimate defaults are anyway given by the framework at the points where the Pars... class is defined, but since at those points there is no knowledge about the details of the problem, these cannot always qualify as “sensible”. |
| [3] | This can be useful e.g. in the case of a complex atom, which has internal structure and motional degrees of freedom. These two are defined as separate elements, and we can use a BinarySystem to actually represent an atom with inner and outer degrees of freedom. |